Staatscourant van het Koninkrijk der Nederlanden
| Datum publicatie | Organisatie | Jaargang en nummer | Rubriek |
|---|---|---|---|
| Ministerie van Onderwijs, Cultuur en Wetenschap | Staatscourant 2023, 6985 | ander besluit van algemene strekking |
Zoals vergunningen, bouwplannen en lokale regelgeving.
Adressen en contactpersonen van overheidsorganisaties.
U bent hier:

| Datum publicatie | Organisatie | Jaargang en nummer | Rubriek |
|---|---|---|---|
| Ministerie van Onderwijs, Cultuur en Wetenschap | Staatscourant 2023, 6985 | ander besluit van algemene strekking |
Het College voor toetsen en examens,
Gelet op artikel 2, tweede lid, aanhef en onderdeel e, van de Wet College voor toetsen en examens;
Gezien de goedkeuring van de Minister voor Primair en Voortgezet Onderwijs, gegeven op 23 februari 2023 met nummer 35821201,
Besluit:
Bijlage 1 van de Regeling omzetting scores in cijfers VO wordt vervangen door de bijlage bij deze regeling.
Deze regeling zal met de toelichting in de Staatscourant worden geplaatst.
Het College voor toetsen en examens, de voorzitter, J.H. van der Vegt
Uitgangspunt
De normering van de centrale examens dient er zorg voor te dragen dat in opeenvolgende jaren aan kandidaten bij een zelfde vak in hetzelfde schooltype of dezelfde leerweg dezelfde eisen worden gesteld.
Omdat het technisch onmogelijk is onze examens van jaar op jaar ‘precies even moeilijk' te maken, zorgt de keuze van de normeringsterm (N-term) daarvoor. Het proces van normering is erop gericht, gegeven dit uitgangspunt, de juiste normeringsterm te bepalen.
In supplement I staan de vergelijkingen die bij de omzetting van score naar cijfer worden gehanteerd.
Bij ieder centraal examen stelt het College voor Toetsen en Examens (CvTE) een referentie-examen vast, zodra dat kan. Een referentie-examen is een examen dat door CvTE en veld wordt gezien als een ‘goed’ examen.
Examens in het eerste tijdvak of de afnameperiode1
Een normering gericht op gelijke cijfers als in voorgaande jaren (relatief normeren) is het startpunt. Om een te strenge of juist te soepele normering te voorkomen zal Stichting Cito Instituut voor Toetsontwikkeling (Stichting Cito) aanvullende gegevens inzetten naast de reeds beschikbare data, zoals:
− Docentenoordeel over de moeilijkheid van het examen, en
− Historische N-term.
Als een examen een onvolkomenheid bevat die kandidaten aanwijsbaar kan benadelen, krijgen correctoren nadere instructies door een aanvulling op het correctievoorschrift.
Examens in het tweede tijdvak
In het tweede tijdvak geldt in beginsel de normeringsterm van het eerste tijdvak. Aan de hand van de statistisch te verwachten resultaatverbetering van kandidaten die in het eerste tijdvak een onvoldoende hadden, wordt nagegaan of deze normeringsterm zou leiden tot hogere eisen aan de kandidaat dan in het eerste tijdvak. Als dat het geval is, wordt de normeringsterm zo vastgesteld dat de eisen gelijk zijn.
Examens in het derde tijdvak
Bij het derde tijdvak wordt de normeringsterm bepaald aan de hand van een gewogen oordeel over de moeilijkheidsgraad, samengesteld uit de oordelen van Stichting Cito, van het CvTE en van de correctoren van deze examens. Hierbij wordt de moeilijkheidsgraad gerelateerd aan de moeilijkheidsgraad van de examens in het eerste tijdvak.
Compensatie voor fouten of onvolkomenheden via de normeringsterm
Voor de voor een kandidaat nadelige gevolgen van een door het CvTE vastgestelde fout of onvolkomenheid in een examen of correctievoorschrift, compenseert het CvTE via de normeringsterm indien:
a. de fout of onvolkomenheid niet eerder is hersteld via een erratum op de opgaven of via een aanvulling op het correctievoorschrift, bedoeld in artikel 10 van de Regeling beoordelingsnormen en bijbehorende scores centraal examen VO;
b. herstel via een aanvulling op het correctievoorschrift gelet op het tijdstip waarop de fout wordt vastgesteld naar het oordeel van het CvTE leidt tot een te groot risico op onjuistheden bij het vaststellen van scores op examens; en
c. de normeringsterm nog niet is vastgesteld.
Deze correctieprocedure via de normeringsterm geldt voor alle tijdvakken en vindt in voorkomende gevallen plaats op grond van de in supplement II bij deze bijlage opgenomen formules voor het compenseren voor een fout of onvolkomenheid in respectievelijk het eerste, tweede en derde tijdvak. Hierdoor wordt voorkomen dat de score van een kandidaat in een te laag cijfer wordt omgezet.
De formules voor de omzetting van score naar cijfer
De huidige regels zijn in 1999 vastgesteld en voor het eerst toegepast bij de examens van 2000. [CEVO-99/648 van 22 juni 1999, Gele katern 1999, nr. 18a].
Uitgangspunten
Het systeem voor de omzetting van score naar cijfer is gebaseerd op de volgende vier uitgangspunten:
1. Elk gescoord punt draagt altijd bij tot een hoger examencijfer (afronding daargelaten);
2. Een score van 0% correspondeert altijd met examencijfer 1,0;
3. Een score van 100% correspondeert altijd met examencijfer 10,0;
4. Over een zo breed mogelijk centraal interval van de scoreschaal is er (afronding daargelaten) sprake van een evenredige stijging van score- en cijferpunten die onafhankelijk is van de normering.
Hierbij wordt onder de score verstaan: de zuivere score, dus uitsluitend de punten die aan de kandidaat zijn toegekend voor goede antwoordelementen.
Er zal derhalve geen sprake meer zijn van scorepunten-vooraf en/of scorepunten-bijtelling (in geval van cesuuraanpassing).
Het normeringsvoorschrift
Het normeringsvoorschrift bestaat uit twee onderdelen:
− de hoofdrelatie: de formule die, voor de overgrote meerderheid der kandidaten, het berekeningsvoorschrift geeft voor het omzetten van score naar cijfer;
− vier grensrelaties: vier formules die (bij andere N-termen dan 1,0) voorkomen dat kandidaten met zeer lage of zeer hoge scores een cijfer zouden krijgen dat in strijd is met bovengenoemde vier uitgangspunten.
De hoofdrelatie
De hoofdrelatie geeft aldus het examencijfer als functie van de score:
C = 9,0 * (S/L) + N.................... (1)
waarin:
C = het cijfer voor het centraal examen.
S = de score, dat wil zeggen de zuivere aan de kandidaat toegekende score.
L = de lengte van de scoreschaal, zoals vastgelegd in het correctievoorschrift;
N = de normeringsterm, liggend tussen de waarden: N = 0,0 en N = 2,0, vast te stellen door het College voor Toetsen en Examens middels een normeringsbeslissing.
Zijn zowel L als N bekend, dan leidt invullen van de score S direct tot het examencijfer C.
Voorbeeld:
Stel de lengte van de scoreschaal is L = 90 punten;
dan gaat formule (1) over in:
C = 9,0 * (S/90) + N.
Voordat hiermee uit score S examencijfer C kan worden berekend, moet het College voor Toetsen en Examens eerst een waarde voor normeringsterm N hebben vastgesteld.
Stel dat wordt: N = 1,0; dan krijgt formule (1) zijn definitieve vorm:
C = 9,0 * (S/90) + 1,0.
Deze is gevisualiseerd in figuur 1: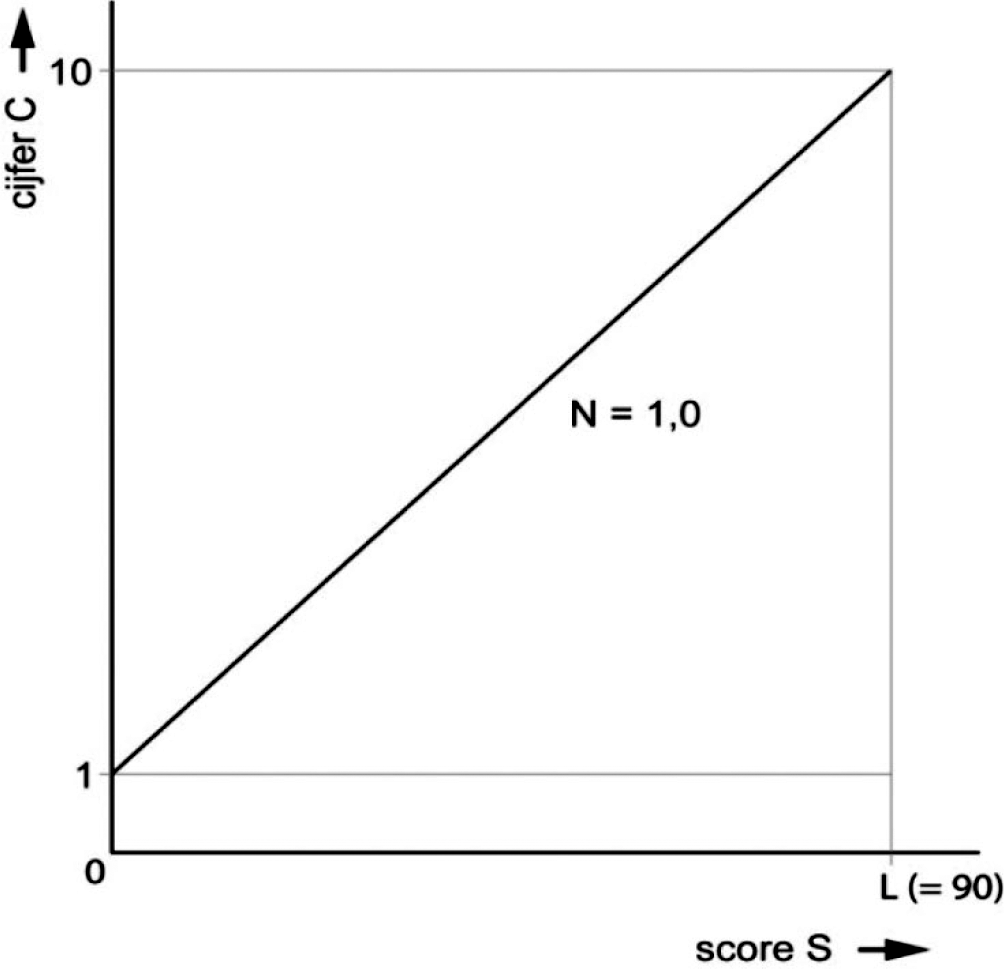
figuur 1
Concreet: drie kandidaten met scores van resp. 0%, 50% en 100% – wat bij deze L van 90 pt correspondeert met scores van 0, 45 en 90 pt – zouden achtereenvolgens de examencijfers: 1,0, 5,5 en 10,0 krijgen. Als was gekozen voor een andere schaallengte, bv L = 68, dan zou formule (1), – bij dezelfde N-term N = 1,0) overgaan in:
C = 9,0 * (S/68) + 1,0.
Nu zouden genoemde drie kandidaten voor dezelfde examencijfers (1,0, 5,5 en 10,0) respectievelijk de scores 0, 34 en 68 nodig hebben!
De grensrelaties
Deze zijn nodig om de boven gegeven vier uitgangspunten óók te kunnen eerbiedigen als de normeringsterm N groter of kleiner is dan 1,0.
Voorbeeld:
Bij een waarde voor de normeringsterm van N = 1,3, zouden de drie kandidaten met scores 0%, 50% en 100% op grond van de hoofdrelatie resp. de cijfers 1,3, 5,8 en 10,3 krijgen;
daarvan is echter het eerste cijfer guller dan de bedoeling en is het derde cijfer hoger dan het toegestane maximum.
Iets dergelijks treedt op bij een normeringsterm lager dan 1,0, bijvoorbeeld: N = 0,7. Genoemde drie kandidaten zouden in dat geval de examencijfers 0,7, 5,2 en 9,7 krijgen, waarvan het eerste cijfer uitkomt onder het toegestane minimum en het derde cijfer lager is dan de verdiende 10,0!
Deze problematiek is in beeld gebracht in figuur 2: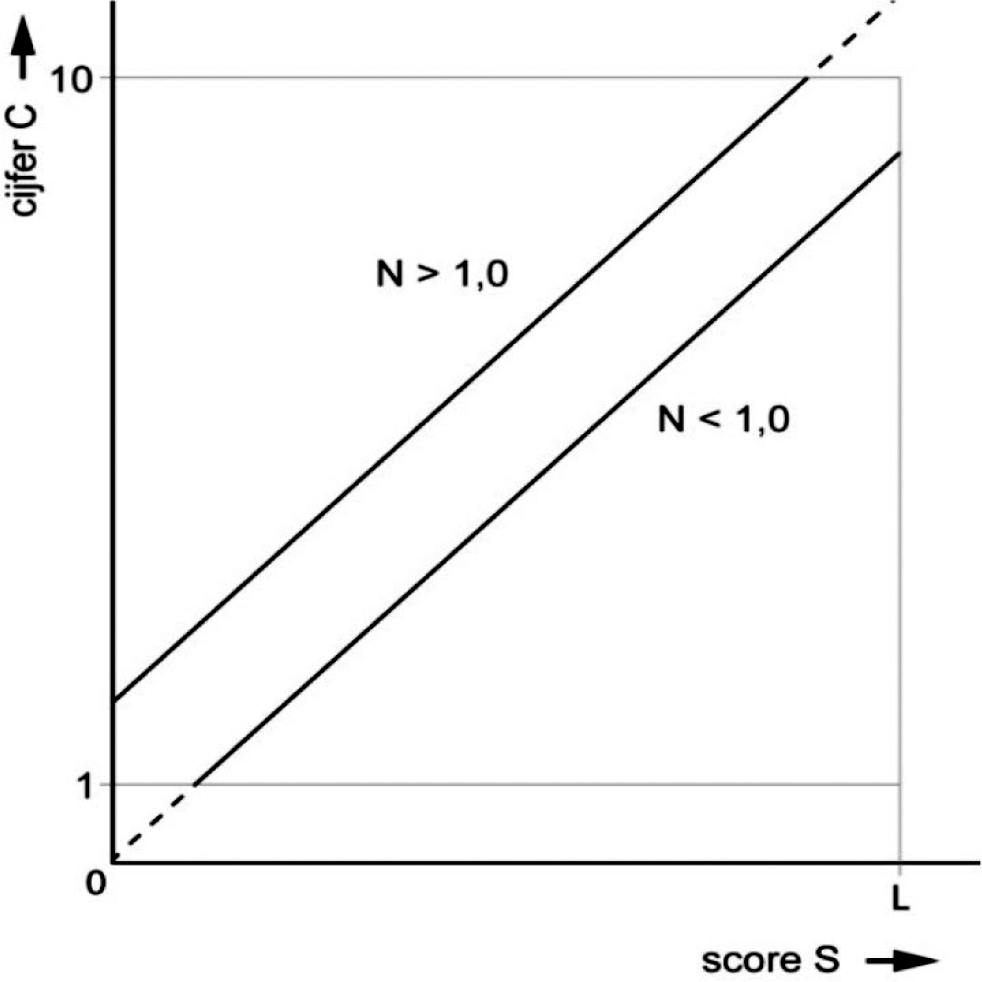
figuur 2
Deze ‘bijzonderheden’ worden verholpen door middel van een systeem van zogeheten grensrelaties.
Het principe van grensrelaties is gevisualiseerd in figuur 3. Bij voorbaat zullen
alle score-cijfercombinaties liggen binnen het gebied dat begrensd wordt door de vier
lijnstukken in deze figuur.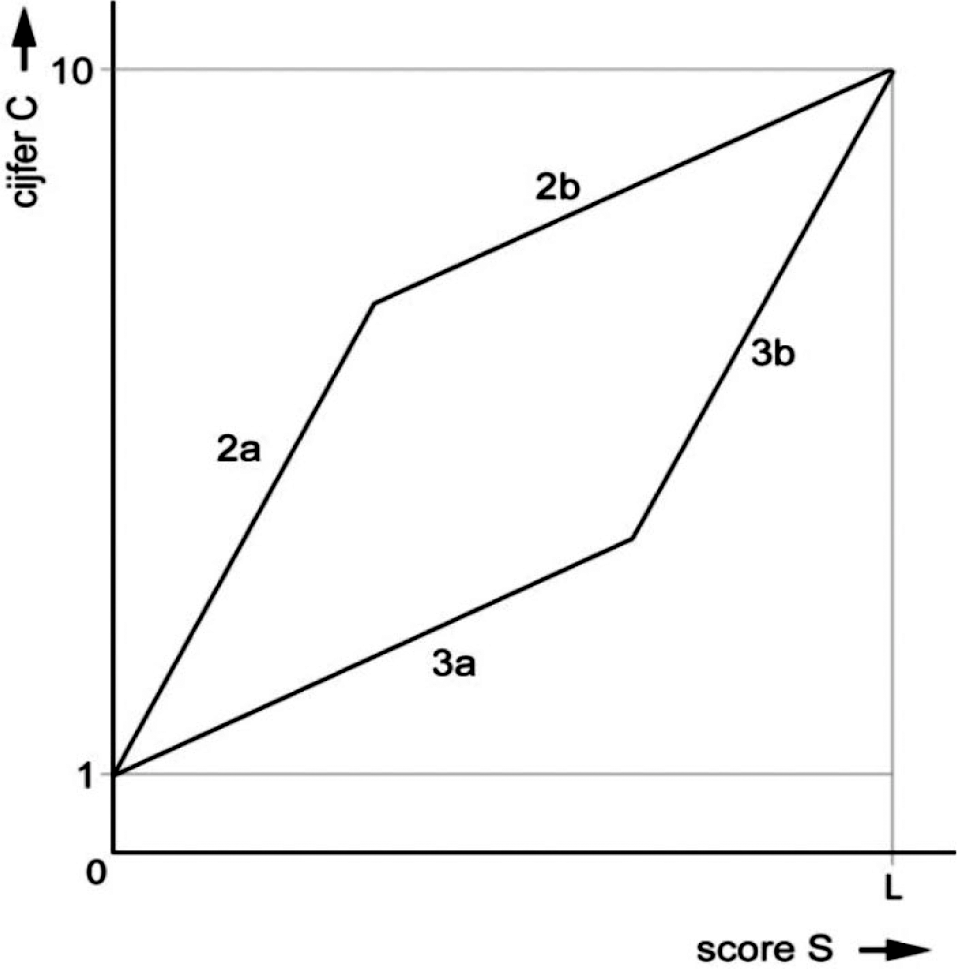
figuur 3
Samen vormen de vier lijnstukken 2a, 2b, 3a en 3b een ‘venster’ waarbinnen alle toegestane score-cijfercombinaties moeten liggen. Dreigt bij toepassing van de hoofdrelatie – formule (1) – een score-cijfercombinatie buiten deze grenzen te vallen, dan moet voor de desbetreffende score dat cijfer vervangen worden door het cijfer berekend met de corresponderende grensrelatie. Wat informeler gezegd: score-cijfercombinaties die buiten het ‘venster’ dreigen te vallen, komen op het ‘kozijn’ terecht.
De grensrelaties worden gevormd door de volgende vier formules:
C = 1,0 + S* (9/L)*2.......................... (2a)
C = 10,0 – (L-S)* (9/L) * 0,5................. (2b)
C = 1,0 + S* (9/L)* 0,5.........................(3a)
C = 10,0 – (L-S)*(9/L)*2.................... (3b)
Bij N > 1,0 geldt voor de laagste scores de formule (2a) en voor de hoogste scores de formule (2b).
In figuur 4 is dit gevisualiseerd.
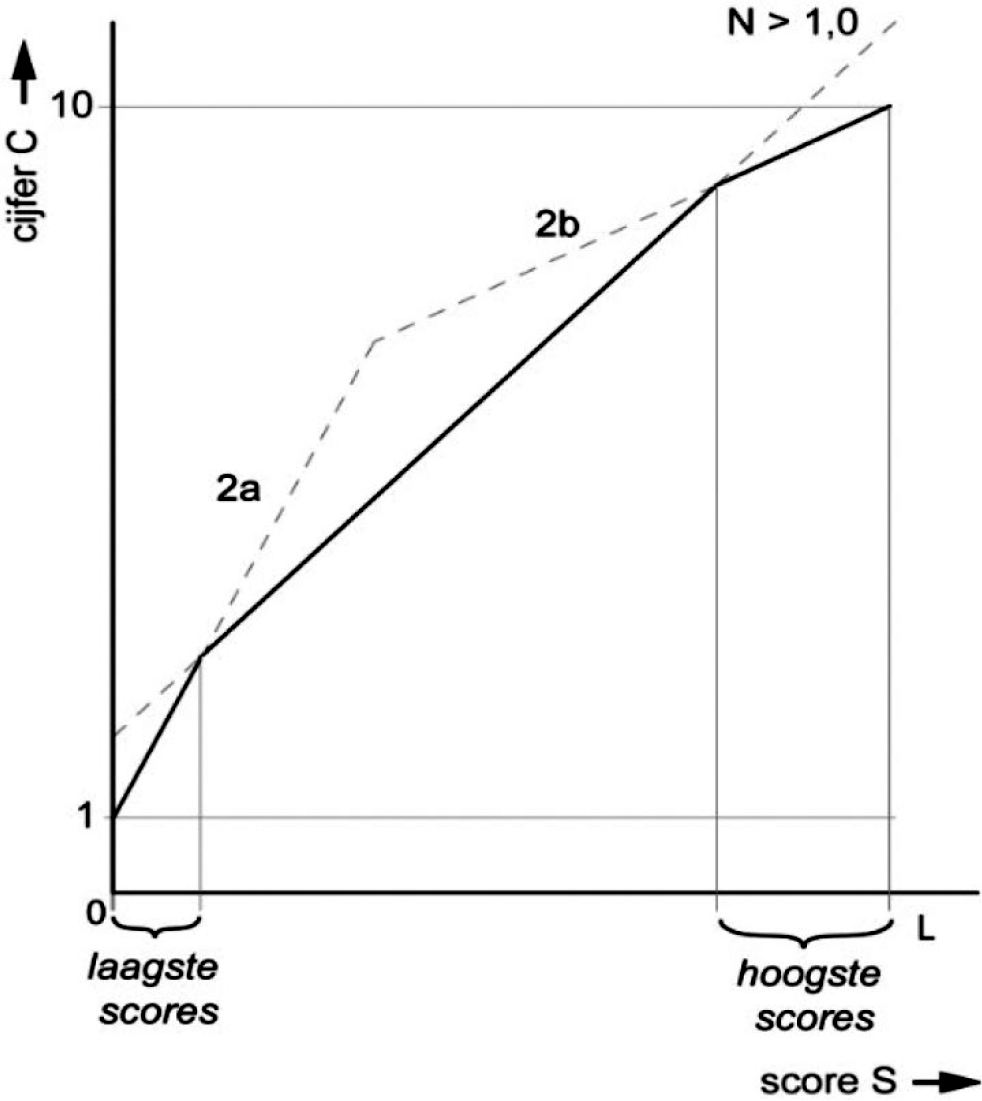
figuur 4
Bij N < 1,0 geldt voor de laagste scores de formule (3a) en voor de hoogste scores de formule (3b).
In figuur 5 is dit gevisualiseerd.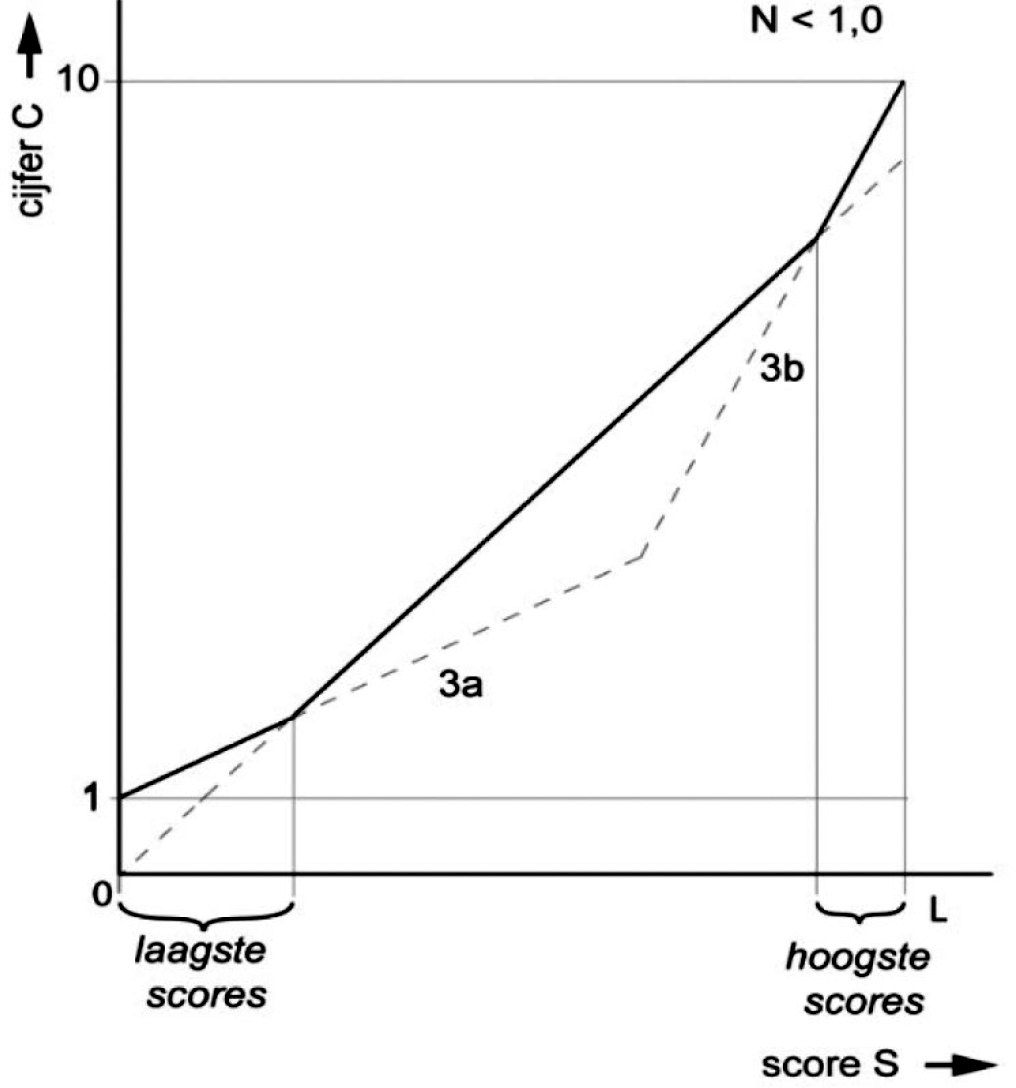
figuur 5
Bij een waarde voor de normeringsterm van N = 1,0 treedt het systeem van grensrelaties niet in werking en resulteert een score-cijfertransformatie die grafisch wordt gerepresenteerd door de rechte lijn van Fig.1, de lijn die in Fig. 4 is gelabeld met: ‘N=1,0’.
Bij alle andere waarden van N zijn de grensrelaties wel van belang. In figuur 6 zijn
als voorbeelden de twee uiterste gevallen in beeld gebracht, die resp. corresponderen
met de normeringsbeslissingen N = 2,0 en N = 0,0. Deze leveren als score-cijfertransformaties
de twee dubbel-geknikte lijnen op (gelabeld met ‘N=2,0’ en ‘N=0,0’).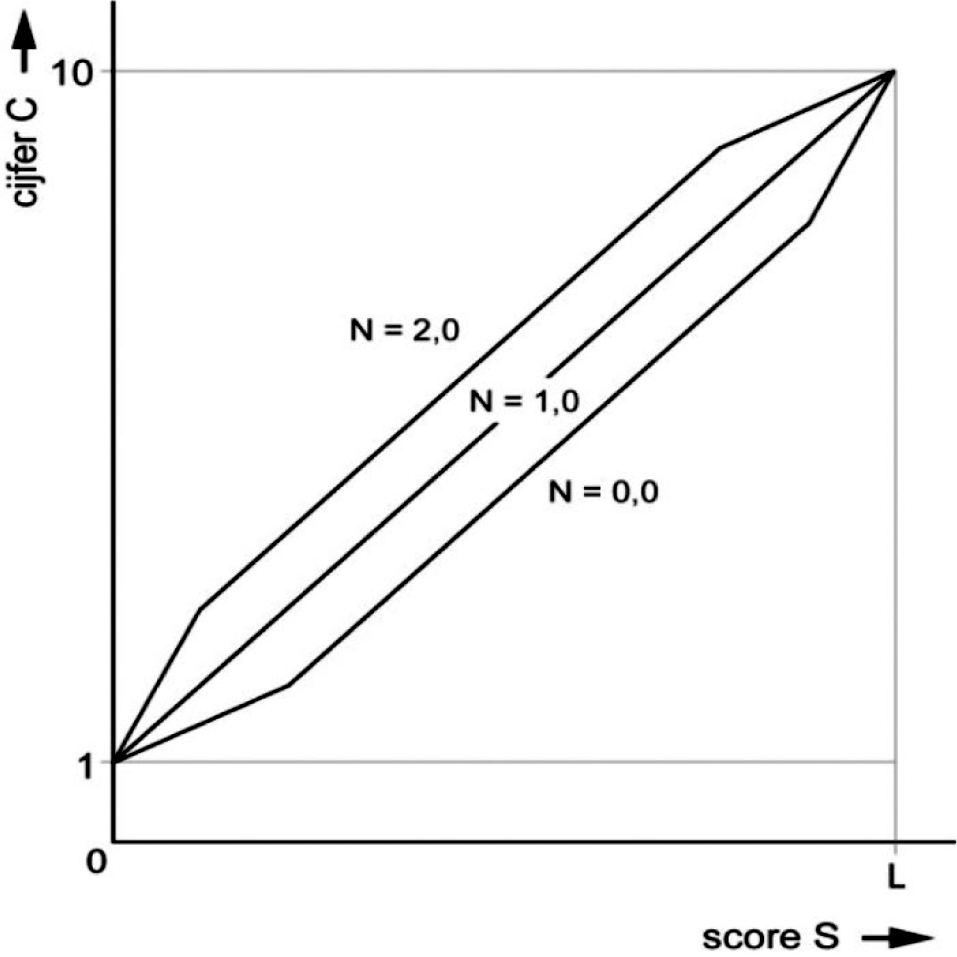
figuur 6
De formules voor het compenseren voor een fout of onvolkomenheid
Examens in het eerste tijdvak
De N-term die zou zijn vastgesteld als de desbetreffende fout of onvolkomenheid in een examen of correctievoorschrift niet door het CvTE was vastgesteld, wordt verhoogd met 9 * Pvrg * Mvrg / L, waarbij deze uitkomst wordt afgerond op één decimaal.
In deze formule staat Pvrg voor de P-waarde van de onvolkomen vraag en Mvrg voor de maximaal haalbare score op deze vraag. Een P-waarde van 0,63 betekent dat de kandidaten gemiddeld 63% van Mvrg behaald hebben. L staat voor de lengte van de scoreschaal oftewel de maximaal haalbare score op het gehele examen.
Het uitgangspunt bij deze werkwijze is dat de kandidaat die geen punten heeft kunnen scoren op de onvolkomen vraag, precies voldoende wordt gecompenseerd.
Examens in het tweede tijdvak
In het tweede tijdvak wordt van het ingekorte examen, dus zonder de foute of onvolkomen vraag, P-ir berekend. De N-term die in eerste instantie zonder de fout zou zijn vastgesteld, wordt verhoogd met 9 * P-ir * Mvrg / L, waarbij deze uitkomst wordt afgerond op één decimaal.
Deze verhoging voorkomt dat de onvolkomen vraag tot een te lage N-term zou leiden.
Examens in het derde tijdvak
Aan het derde tijdvak nemen zo weinig kandidaten deel dat de P-waarden geen relevante informatiebron vormen. De N-term die zonder de fout zou zijn vastgesteld wordt verhoogd met 9 * Mvrg / L. Dit komt erop neer dat in het derde tijdvak gewerkt wordt met een Pvrg en een P-ir van 1.
De Minister heeft de Tweede Kamer met zijn brief van 21 november 20222 geïnformeerd over diens besluit om in 2023, anders dan in 2021 en 2022, geen derde tijdvak voor de afnamen van centrale examens op de scholen toe te staan. De wijze van normeren in het eerste tijdvak blijft gelijk aan die van de afgelopen twee jaren. De wijze van normeren in het tweede en derde tijdvak wordt weer gedaan zoals voor Corona. Dat betekent dat de regeling op de volgende punten zal worden aangepast.
Ondanks dat vrijwel alle kandidaten hun centrale examens in het eerste tijdvak zullen maken, kan het College voor toetsen en examens dit schooljaar nog niet vaststellen of het vaardigheidsniveau van de examenleerlingen hetzelfde is als in de jaren 2015 tot en met 2019. Het College heeft daarom besloten de wijze van normeren in 2021 en 2022 voort te zetten in 2023. Meer informatie hierover is te vinden op Examenblad.nl.
Door het wegvallen van de spreidingsmogelijkheid kan de herkansingsnormering weer worden toegepast zoals dit voor Corona ook gebeurde. Er zullen ook weer voorlopige N-termen voor het tweede tijdvak gepubliceerd worden gelijktijdig met de N-termen van het eerste tijdvak.
Het derde tijdvak op de scholen is komen te vervallen. Het derde tijdvak bij de Staatsexamens vo zal op dezelfde wijze genormeerd worden als voor Corona. De moeilijkheidsgraad van de examens wordt vergeleken met de moeilijkheidsgraad van de examens in het eerste tijdvak.
In het tweede tijdvak kan voor het bepalen van de hoogte van de compensatie voor een onvolkomen vraag weer de formule gehanteerd worden die alleen gebaseerd is op de herkansende leerlingen. De formule voor het derde tijdvak op de scholen is komen te vervallen.
Het College voor toetsen en examens, de voorzitter, J.H. van der Vegt
De flexibele en digitale centrale examens voor de algemene vakken in de basisberoepsgerichte leerweg en kaderberoepsgerichte leerweg van het vmbo kennen geen eerste tijdvak maar een afnameperiode.
Kopieer de link naar uw clipboard
https://zoek.officielebekendmakingen.nl/stcrt-2023-6985.html
De hier aangeboden pdf-bestanden van het Staatsblad, Staatscourant, Tractatenblad, provinciaal blad, gemeenteblad, waterschapsblad en blad gemeenschappelijke regeling vormen de formele bekendmakingen in de zin van de Bekendmakingswet en de Rijkswet goedkeuring en bekendmaking verdragen voor zover ze na 1 juli 2009 zijn uitgegeven. Voor pdf-publicaties van vóór deze datum geldt dat alleen de in papieren vorm uitgegeven bladen formele status hebben; de hier aangeboden elektronische versies daarvan worden bij wijze van service aangeboden.
