Staatscourant van het Koninkrijk der Nederlanden
| Datum publicatie | Organisatie | Jaargang en nummer | Rubriek | Datum ondertekening |
|---|---|---|---|---|
| Ministerie van Infrastructuur en Waterstaat | Staatscourant 2022, 103 | algemeen verbindend voorschrift (ministeriële regeling) |
Zoals vergunningen, bouwplannen en lokale regelgeving.
Adressen en contactpersonen van overheidsorganisaties.
U bent hier:

| Datum publicatie | Organisatie | Jaargang en nummer | Rubriek | Datum ondertekening |
|---|---|---|---|---|
| Ministerie van Infrastructuur en Waterstaat | Staatscourant 2022, 103 | algemeen verbindend voorschrift (ministeriële regeling) |
De Minister van Infrastructuur en Waterstaat en de Staatssecretaris van Infrastructuur en Waterstaat,
Gelet op de artikelen 8a.45, vijfde lid, 8a.46, tweede lid, en 8a.48, vierde lid, van de Wet luchtvaart, 11.5 en 11.8, eerste lid, van de Wet milieubeheer, 27 van het Besluit geluid milieubeheer, en 3.9 en 4.22 van het Besluit geluidhinder;
BESLUITEN:
Hoofdstuk 2 van bijlage VII bij het Reken- en meetvoorschrift geluid 2012 komt te luiden:
Berekeningen van de geluidsbelasting worden in het frequentiegebied van 63 Hz tot 8 kHz octaafbanden bepaald. De resultaten van de frequentieband worden op het overeenkomstige frequentie-interval verstrekt.
Berekeningen worden voor wegverkeerslawaai, spoorweglawaai en industrielawaai in octaafbanden uitgevoerd, met uitzondering van het geluidsvermogen van de bron van spoorweglawaai, dat van tertsbanden gebruikmaakt. Voor wegverkeerslawaai, spoorweglawaai en industrielawaai wordt, op basis van de resultaten van deze octaafband, het A-gewogen gemiddelde geluidsniveau over lange termijn voor de dag, de avond en nachtperiode, als vastgesteld in bijlage I en bedoeld in artikel 5 van Richtlijn 2002/49/EG, berekend door de methode beschreven in de punten 2.1.2, 2.2, 2.3, 2.4 en 2.5. Voor het weg- en spoorwegverkeer in agglomeraties wordt het A-gewogen gemiddelde geluidsniveau op lange termijn bepaald op basis van de bijdragen daaraan van de daarin gelegen weg- en spoorwegsegmenten, met inbegrip van de grote wegen en de grote spoorwegen.
|
|
(2.1.1) |
waarbij
Ai de A-gewogen correctie volgens IEC 61672-1 aanduidt,
i de frequentieband-index is,
en T de tijdsperiode is die overeenkomt met dag, avond of nacht.
Geluidsparameters zijn:
|
Lp |
Niveau van momentane geluidsdruk |
[dB] (re. 2 10-5 Pa) |
|
LAeq,LT |
Globaal langdurig geluidsniveau LAeq als gevolg van alle bronnen en spiegelbronnen op punt R |
[dB] (re. 2 10-5 Pa) |
|
LW |
In situ geluidsvermogensniveau van een puntbron (bewegende of stilstaande) |
[dB] (re. 10-12 W) |
|
LW,i,dir |
Richtingsafhankelijk in situ geluidsvermogensniveau voor de i-de-frequentieband |
[dB] (re. 10-12 W) |
|
LW’ |
Gemiddelde in situ geluidsvermogensniveau per meter bronlijn |
[dB/m] (re. 10-12 W) |
Andere fysische parameters zijn:
|
p |
Effectieve waarde van de momentane geluidsdruk |
[Pa] |
|
p0 |
Referentiegeluidsdruk = 2 10-5 Pa |
[Pa] |
|
W0 |
Referentiegeluidsvermogen = 10-12 W |
[Watt] |
Nauwkeurigheid van invoerwaarden
Alle invoerwaarden die het emissieniveau van een bron beïnvloeden, worden bepaald met ten minste de nauwkeurigheid die overeenkomt met een onzekerheid van ± 2dB(A) in het emissieniveau van de bron (waarbij alle andere parameters ongewijzigd blijven).
Gebruik van standaardwaarden
Bij de toepassing van de in dit hoofdstuk weergegeven methode geven de invoergegevens het werkelijke verbruik weer. In principe wordt geen gebruik gemaakt van standaardinvoerwaarden of veronderstellingen. Standaardinvoerwaarden en veronderstellingen worden geaccepteerd indien de verzameling van werkelijke gegevens met onevenredig hoge kosten gepaard gaat.
De kwaliteit van de software die voor de berekeningen wordt gebruikt
Voor de software die voor de berekeningen wordt gebruikt, moet worden bewezen dat aan de hierbij beschreven methode is voldaan, en wel door middel van certificering van resultaten tegen testcases.
Indeling van voertuigen
De bron van wegverkeerslawaai wordt vastgesteld door de geluidsemissies van alle individuele voertuigen van de verkeersstroom te combineren. Deze voertuigen worden ingedeeld in vier verschillende categorieën met betrekking tot de kenmerken van hun geluidsemissie:
Categorie 1: Lichte motorvoertuigen
Categorie 2: Middelzware voertuigen
Categorie 3: Zware voertuigen
Categorie 4: Gemotoriseerde tweewielers
Bij gemotoriseerde tweewielers worden twee afzonderlijke subcategorieën gedefinieerd voor bromfietsen en krachtigere motorfietsen, omdat zij in zeer verschillende rij-modi functioneren en hun aantallen meestal sterk uiteenlopen.
Gebruik van de eerste vier categorieën is verplicht. Er wordt rekening gehouden met de mogelijkheid dat in de toekomst nieuwe voertuigen worden ontwikkeld waarvan de geluidsemissies dusdanig anders zijn dat een extra categorie moet worden vastgesteld. Deze categorie kan betrekking hebben op, bijvoorbeeld, elektrische of hybride voertuigen of andere voertuigen die in de toekomst worden ontwikkeld en die wezenlijk verschillen van de voertuigen in de categorieën 1 tot en met 4.
De bijzonderheden van de verschillende voertuigcategorieën worden in tabel 2.2.a vermeld.
|
Categorie |
Naam |
Beschrijving |
Voertuigcategorie in EU Goedkeuring van volledige voertuigen 1 |
||
|---|---|---|---|---|---|
|
1 |
Lichte motorvoertuigen |
Personenauto's, bestelwagens ≤ 3,5 ton, SUV's2, MPV's3, waaronder aanhangers en caravans |
M1 en N1 |
||
|
2 |
Middelzware voertuigen |
Middelzware voertuigen, bestelwagens > 3,5 ton, bussen, campers enz., met twee assen en dubbele banden op de achteras |
M2, M3 en N2, N3 |
||
|
3 |
Zware voertuigen |
Zware bedrijfsvoertuigen, touringcars, bussen, met drie of meer assen |
M2 en N2 met aanhangwagen, M3 en N3 |
||
|
4 |
Gemotoriseerde tweewielers |
4a |
Bromfietsen met twee, drie of vier wielen |
L1, L2, L6 |
|
|
4b |
Motorfietsen met of zonder zijspan, driewielers en vierwielers |
L3, L4, L5, L7 |
|||
Richtlijn 2007/46/EG van het Europees parlement en de Raad van 5 september 2007 tot vaststelling van een kader voor de goedkeuring van motorvoertuigen en aanhangwagens daarvan en van systemen, onderdelen en technische eenheden die voor dergelijke voertuigen zijn bestemd (PBEU, 2007, L 263, van 9 oktober 2007).
Aantal en plaats van equivalente geluidsbronnen
In dit model wordt elk voertuig (categorieën 1, 2, 3, 4a en 4b) weergegeven met één enkele puntbron die gelijkmatig afstraalt. De eerste reflectie op het wegdek wordt impliciet behandeld. Zoals afgebeeld in figuur 2.2.a, wordt deze puntbron 0,05 m boven het wegdek geplaatst.
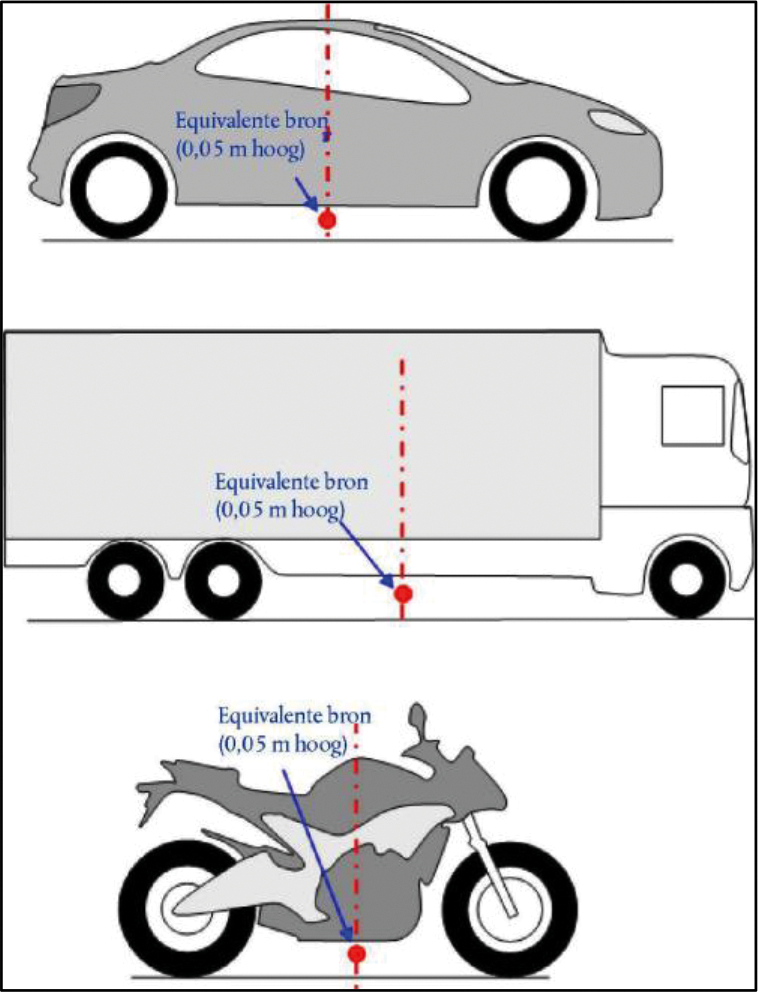
Figuur 2.2.a, Locatie van equivalente puntbron op lichte voertuigen (categorie 1), zware voertuigen (categorieën 2 en 3) en tweewielers (categorie 4)
De verkeersstroom wordt door een bronlijn weergegeven. Bij het modelleren van een weg met meerdere rijbanen, wordt elke rijbaan idealiter door een bronlijn in het midden van elke rijbaan weergegeven. Het is echter ook aanvaardbaar om één bronlijn in het midden van een tweebaansweg of één bronlijn per rijbaan in de buitenste baan van meerbaanswegen te modelleren.
Inleiding
Het geluidsvermogen van de bron wordt in het ‘half-vrije veld’ gedefinieerd, aldus omvat het geluidsvermogen het effect van de reflectie van de grond onmiddellijk onder de gemodelleerde bron waar zich geen verstorende objecten in de onmiddellijke omgeving bevinden, met uitzondering van de reflectie op het wegdek niet onmiddellijk onder de gemodelleerde bron.
Verkeersstroom
De geluidsemissie van een verkeersstroom wordt weergegeven door een bronlijn, gekenmerkt door haar richtingsafhankelijk geluidsvermogen per meter per frequentie. Dit komt overeen met de som van de geluidsemissie van de individuele voertuigen in de verkeersstroom, rekening houdend met de tijd die de voertuigen in het beschouwde wegvak zijn. De uitvoering van het individuele voertuig in de stroom vereist de toepassing van een verkeersstroommodel.
Als een constante verkeersstroom van Qm voertuigen van categorie m per uur wordt verondersteld, met een gemiddelde snelheid νm (in km/h), wordt het richtingsafhankelijk geluidsvermogen per meter in de frequentieband i van de bronlijn LW’,eq,lijn,i,m bepaald door:
|
|
(2.2.1) |
waarbij LW,i,m het gerichte geluidsvermogen van een enkel voertuig is. LW’,m wordt uitgedrukt in dB (re. 10-12 W/m). Deze geluidsvermogensniveaus worden berekend voor elke octaafband i van 63 Hz tot en met 8 kHz.
De verkeersstroomgegevens Qm worden als jaargemiddelde per uur, per tijdsperiode (dag-avond-nacht), per voertuigklasse en per bronlijn uitgedrukt. Voor alle categorieën worden verkeersstroom-invoergegevens afkomstig van verkeerstelling of verkeersmodellen gebruikt.
De snelheid νm is een representatieve snelheid per voertuigcategorie: in de meeste gevallen is dat de wettelijke maximumsnelheid voor het wegvak of, als dit lager is, de wettelijke maximumsnelheid voor de voertuigcategorie.
Individueel voertuig
Aangenomen wordt dat alle voertuigen van categorie m in de verkeersstroom op dezelfde snelheid rijden, dat wil zeggen νm.
Een wegvoertuig wordt gemodelleerd door een aantal wiskundige vergelijkingen die de twee belangrijkste bronnen van lawaai weergeven:
1. rolgeluid als gevolg van de wisselwerking tussen band en wegoppervlak;
2. aandrijfgeluid veroorzaakt door de aandrijflijn (motor, uitlaat enz.) van het voertuig.
Aerodynamisch geluid wordt in de bron van het rolgeluid opgenomen.
Voor lichte, middelzware en zware voertuigen (categorieën 1, 2 en 3) komt het totale geluidsvermogen overeen met de energetische som van het rolgeluid en het aandrijfgeluid. Het totale geluidsvermogensniveau van de bronlijnen m = 1, 2 of 3 wordt dus gedefinieerd door:
|
|
(2.2.2) |
waarbij LWR,i,m het geluidsvermogensniveau voor rolgeluid en LWP,i,m het geluidsvermogensniveau voor aandrijfgeluid is. Dit geldt voor alle snelheidsbereiken.
Voor snelheden minder dan 20 km/h heeft het totale geluidsvermogen voor een voertuig hetzelfde geluidsvermogensniveau als door de formule voor νm = 20 km/h wordt bepaald.
Voor tweewielers (categorie 4) wordt alleen aandrijfgeluid aangemerkt voor de bron:
|
LWR,i,m =4 (νm= 4) = LWP,i,m=4 (νm= 4) |
(2.2.3) |
Dit geldt voor alle snelheidsbereiken. Voor snelheden minder dan 20 km/h heeft het totale geluidsvermogen voor een voertuig hetzelfde geluidsvermogensniveau als door de formule voor νm = 20 km/h wordt bepaald.
De bronvergelijkingen en coëfficiënten gelden voor de volgende referentieomstandigheden:
• een constante voertuigsnelheid,
• een vlakke weg,
• een luchttemperatuur van τref = 20°C,
• een virtueel referentiewegdek, bestaand uit gemiddeld dicht asfaltbeton 0/11 en steenmastiekasfalt 0/11, tussen 2 en 7 jaar oud en in een representatieve onderhoudstoestand,
• een droog wegdek,
• geen spijkerbanden.
Algemene vergelijking
Het geluidsvermogensniveau van rolgeluid in de frequentieband i voor een voertuig van categorie m = 1, 2 of 3 wordt gedefinieerd als:
|
|
(2.2.4) |
De coëfficiënten AR,i,m en BR,i,m worden voor elke voertuigcategorie in octaafbanden en voor een referentiesnelheid νref = 70 km/h gegeven. ∆LWR,i,m stemt overeen met de som van de correctiecoëfficiënten die worden toegepast op de rolgeluidemissie voor specifieke weg- of voertuigomstandigheden die van de referentieomstandigheden afwijken:
|
∆LWR,i,m = ∆LWR,road,i,m + ∆LWR,acc,i,m + ∆LW,temp |
(2.2.5) |
∆LWR,road,i,m verdisconteert het effect op het rolgeluid van een wegdek met akoestische eigenschappen die verschillen van die van het virtuele referentiewegdek zoals gedefinieerd in hoofdstuk 2.2.2. Dit omvat zowel het effect op voortplanting als het effect op emissie.
∆LWR,acc,i,m verdisconteert het effect op het rolgeluid van een kruising met verkeerslichten of een rotonde. Het integreert het effect van de snelheidsvariatie op de geluidsbelasting.
∆LW,temp is een correctieterm voor een gemiddelde temperatuur τ die verschilt van de referentietemperatuur τref = 20°C.
Effect van luchttemperatuur op rolgeluidcorrectie
De luchttemperatuur heeft invloed op de rolgeluidsemissie; het niveau van het rolgeluidsvermogen neemt af wanneer de luchttemperatuur toeneemt. Dit effect wordt in de wegdekcorrectie ingevoerd. Wegdekcorrecties worden gewoonlijk op een luchttemperatuur van τref = 20°C beoordeeld. Bij een verschillende jaarlijkse gemiddelde luchttemperatuur °C, wordt het wegdekgeluid gecorrigeerd door:
|
∆LW,temp,m,(τ) = Km (τref – τ) |
(2.2.6) |
De correctieterm is positief (dat wil zeggen lawaai neemt toe) voor temperaturen lager dan 20°C en negatief (dat wil zeggen lawaai neemt af) voor hogere temperaturen. De coëfficiënt K is afhankelijk van het wegdek en de kenmerken van de band en vertoont in het algemeen enige afhankelijkheid van frequentie. Een algemene coëfficiënt Km=1 = 0,08 dB/°C voor lichte voertuigen (categorie 1) en Km=2 = Km=3 = 0,04 dB/°C voor zware voertuigen (categorieën 2 en 3) wordt voor alle wegdekken toegepast. De correctiecoëfficiënt wordt in dezelfde mate op alle octaafbanden van 63 tot en met 8.000 Hz toegepast.
Algemene vergelijking
De aandrijfgeluidsemissie omvat alle bijdragen van de motor, uitlaat, versnellingen, luchtinlaat enz. Het vermogensniveau van het aandrijfgeluid in de frequentieband i voor een voertuig van categorie m wordt gedefinieerd als:
|
|
(2.2.7) |
De coëfficiënten AP,i,m en BP,i,m worden voor elke voertuigcategorie in octaafbanden en voor een referentiesnelheid νref = 70 km/h opgegeven.
∆LWP,i,m stemt overeen met de som van de correctiecoëfficiënten die worden toegepast op de aandrijfgeluidsemissie voor specifieke rijomstandigheden of regionale omstandigheden die van de referentieomstandigheden afwijken:
|
∆LWP,i,m = ∆LWP,road,i,m + ∆LWP,grad,i,m + ∆LWP,acc,i,m |
(2.2.8) |
∆LWP,road,i,m verdisconteert het effect van het wegdek op het aandrijfgeluid via absorptie. De berekening wordt volgens hoofdstuk 2.2.6 verricht.
∆LWP,acc,i,m en ∆LWP,grad,i,m veroorzaken het effect van weghellingen en van versnelling en vertraging van voertuigen op kruispunten. Zij worden in overeenstemming met respectievelijk hoofdstukken 2.2.4 en 2.2.5 berekend.
Effect van weghellingen
De weghelling heeft twee gevolgen voor de geluidsemissie van het voertuig. Ten eerste heeft zij invloed op de voertuigsnelheid en dus op de rol- en aandrijfgeluidsemissies van het voertuig. Ten tweede heeft zij invloed op zowel de motorbelasting als het motortoerental via de keuze van versnelling en dus op de aandrijfgeluidsemissie van het voertuig. Alleen het effect op het aandrijfgeluid wordt in deze sectie in aanmerking genomen, waarbij van een constante snelheid wordt uitgegaan.
Voor m=1
|
|
(2.2.9) |
Voor m=2
|
|
(2.2.10) |
Voor m=3
|
|
(2.2.11) |
Voor m=4
|
∆LWP,grad,i,m = 4 = 0 |
(2.2.12) |
De correctie ∆LWP,grad,m houdt impliciet rekening met het effect van de helling op de snelheid.
Voor en na kruispunten met verkeerslichten en rotondes wordt een correctie toegepast voor het effect van versnelling en vertraging zoals hieronder beschreven.
De correctietermen voor rolgeluid, ∆LWR,acc,m,k, en voor aandrijfgeluid, ∆LWP,acc,m,k, zijn lineaire functies van de afstand x (in m) van de puntbron tot het dichtstbijzijnde snijpunt van de respectieve bronlijn met een andere bronlijn. De correctietermen worden in gelijke mate aan alle octaafbanden toegeschreven:
|
|
(2.2.13) |
|
|
(2.2.14) |
De coëfficiënten CR,m,k en CP,m,k hangen af van de aard van het kruispunt k (k = 1 voor een kruispunt met verkeerslichten, k = 2 voor een rotonde) en worden voor elke voertuigcategorie vermeld. De correctie omvat het effect van snelheidsverandering bij het naderen of wegrijden van een kruispunt of rotonde.
Opgemerkt wordt dat op een afstand | x | ≥ 100 m, ∆LWR,acc,m,k = ∆LWP,acc,m,k = 0.
Algemene beginselen
Voor een wegdek met akoestische eigenschappen die afwijken van de akoestische eigenschappen van het referentiewegdek, wordt een spectrale correctieterm voor zowel rolgeluid als aandrijfgeluid toegepast.
De wegdekcorrectieterm voor de rolgeluidsemissie wordt verkregen door:
|
|
(2.2.15) |
waarbij
αi,m de spectrale correctie in dB op referentiesnelheid νref voor categorie m (1, 2 of 3) en spectrale band i is,
βm het effect van de snelheid op de vermindering van het rolgeluid voor categorie m (1, 2 of 3) is, en voor alle frequenties gelijk is.
De wegdekcorrectieterm voor de aandrijfgeluidsemissie wordt verkregen door:
|
∆LWP,road,i,m = min (αi,m; 0) |
(2.2.16) |
Absorberende wegdekken verminderen het aandrijfgeluid, terwijl niet-absorberende oppervlakken het niet vergroten.
Leeftijdseffect op de eigenschappen van het wegdekgeluid
De geluidskenmerken van wegdekken variëren naar gelang de leeftijd en het onderhoudsniveau en worden na verloop van tijd luider. In deze methode worden die wegdekparameters afgeleid die representatief zijn voor de akoestische prestaties van het type wegdek, evenredig verdeeld over de representatieve levensduur en uitgaande van goed onderhoud.
|
Categorie |
Coëfficient |
63 |
125 |
250 |
500 |
1000 |
2000 |
4000 |
8000 |
|---|---|---|---|---|---|---|---|---|---|
|
1 |
AR |
83,4 |
86,8 |
86,1 |
92,5 |
99,8 |
96,6 |
85,8 |
76,2 |
|
BR |
39,2 |
37,5 |
32,2 |
18,4 |
24,9 |
25,8 |
32,1 |
35,1 |
|
|
AP |
98,0 |
90,3 |
89,7 |
88,3 |
86,8 |
89,7 |
85,1 |
78,0 |
|
|
BP |
2,8 |
6,1 |
5,6 |
5,4 |
5,1 |
3,5 |
5,3 |
6,3 |
|
|
2 |
AR |
88,2 |
91,4 |
91,0 |
99,2 |
100,2 |
94,3 |
86,6 |
82,2 |
|
BR |
27,7 |
23,7 |
16,6 |
18,3 |
28,8 |
32,6 |
31,0 |
28,2 |
|
|
AP |
105,3 |
99,4 |
98,5 |
99,4 |
101,5 |
98,6 |
91,7 |
84,6 |
|
|
BP |
–2,4 |
–0,6 |
–1,0 |
3,8 |
5,9 |
5,0 |
3,3 |
1,3 |
|
|
3 |
AR |
90,4 |
93,2 |
94,4 |
104,6 |
105,3 |
98,4 |
89,3 |
83,8 |
|
BR |
30,3 |
26,9 |
22,1 |
26,1 |
33,7 |
35,2 |
35,6 |
34,0 |
|
|
AP |
107,8 |
102,2 |
102,2 |
104,9 |
104,6 |
100,1 |
93,5 |
86,7 |
|
|
BP |
0,8 |
0,3 |
0,3 |
5,6 |
6,2 |
4,4 |
3,9 |
2,3 |
|
|
4a |
AR |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
BR |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
|
AP |
93,0 |
93,0 |
93,5 |
95,3 |
97,2 |
100,4 |
95,8 |
90,9 |
|
|
BP |
4,2 |
7,4 |
9,8 |
11,6 |
15,7 |
18,9 |
20,3 |
20,6 |
|
|
4b |
AR |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
BR |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
|
AP |
99,9 |
101,9 |
96,7 |
94,4 |
95,2 |
94,7 |
92,1 |
88,6 |
|
|
BP |
3,2 |
5,9 |
11,9 |
11,6 |
11,5 |
12,6 |
11,1 |
12,0 |
|
Categorie |
k |
CR |
CP |
|---|---|---|---|
|
1 |
1=kruising |
–4,5 |
5,5 |
|
2=rotonde |
–4,4 |
3,1 |
|
|
2 |
1=kruising |
–4,0 |
9,0 |
|
2=rotonde |
–2,3 |
6,7 |
|
|
3 |
1=kruising |
–4,0 |
9,0 |
|
2=rotonde |
–2,3 |
6,7 |
|
|
4a/4b |
1=kruising |
0,0 |
0,0 |
|
2=rotonde |
0,0 |
0,0 |
|
Beschrijving |
Minimumsnelheid [km/h] |
Maximumsnelheid [km/h] |
Categorie |
αm (63 Hz) |
αm (125 Hz) |
αm (250 Hz) |
αm (500 Hz) |
αm (1 kHz) |
αm (2 kHz) |
αm (4 kHz) |
αm (8 kHz) |
βm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Referentie-wegdek |
-- |
-- |
1 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
2 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
3 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
1-laags Zoab |
50 |
130 |
1 |
0,0 |
5,4 |
4,3 |
4,2 |
–1,0 |
–3,2 |
–2,6 |
0,8 |
-6,5 |
|
2 |
7,9 |
4,3 |
5,3 |
–0,4 |
–5,2 |
–4,6 |
–3,0 |
–1,4 |
0,2 |
|||
|
3 |
9,3 |
5,0 |
5,5 |
–0,4 |
–5,2 |
–4,6 |
–3,0 |
–1,4 |
0,2 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Akoestisch geoptimaliseerd 1L ZOAB |
50 |
130 |
1 |
–0,7 |
0,5 |
1,4 |
3,7 |
-5,2 |
-6,3 |
–5,9 |
–4,7 |
–5,9 |
|
2 |
–1,2 |
–0,3 |
3,6 |
–0,9 |
–7,6 |
–6,0 |
–5,2 |
–4,9 |
–5,5 |
|||
|
3 |
–1,2 |
–0,3 |
3,6 |
–0,9 |
–7,6 |
–6,0 |
–5,2 |
–4,9 |
–5,5 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
2-laags Zoab |
50 |
130 |
1 |
1,6 |
4,0 |
0,3 |
–3,0 |
–4,0 |
–6,2 |
–4,8 |
–2,0 |
–3,0 |
|
2 |
7,3 |
2,0 |
–0,3 |
–5,2 |
–6,1 |
–6,0 |
–4,4 |
–3,5 |
4,7 |
|||
|
3 |
8,3 |
2,2 |
–0,4 |
–5,2 |
–6,2 |
–6,1 |
–4,5 |
–3,5 |
4,7 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
2-laags Zoab (fijn) |
80 |
130 |
1 |
–1,0 |
3,0 |
–1,5 |
–5,3 |
–6,3 |
–8,5 |
–5,3 |
–2,4 |
–0,1 |
|
2 |
7,9 |
0,1 |
–1,9 |
–5,9 |
–6,1 |
–6,8 |
–4,9 |
–3,8 |
–0,8 |
|||
|
3 |
9,4 |
0,2 |
–1,9 |
–5,9 |
–6,1 |
–6,7 |
–4,8 |
–3,8 |
–0,9 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
SMA-NL5 |
40 |
80 |
1 |
10,3 |
–0,9 |
0,9 |
1,8 |
–1,8 |
–2,7 |
–2,0 |
–1,3 |
–1,6 |
|
2 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
3 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
SMA-NL8 |
40 |
80 |
1 |
6,0 |
0,3 |
0,3 |
0,0 |
–0,6 |
–1,2 |
–0,7 |
–0,7 |
–1,4 |
|
2 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
3 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Akoestisch geoptimaliseerd SMA |
40 |
80 |
1 |
6,1 |
–0,9 |
–1,1 |
–0,1 |
–2,9 |
–3,2 |
–3,2 |
–3,0 |
–2,2 |
|
2 |
–3,0 |
–2,4 |
–1,6 |
–2,2 |
–3,0 |
–3,0 |
–3,0 |
–4,0 |
–2,3 |
|||
|
3 |
–3,0 |
–2,4 |
–1,6 |
–2,2 |
–3,0 |
–3,0 |
–3,0 |
–4,0 |
–2,3 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Uitgeborsteld beton |
70 |
120 |
1 |
8,2 |
–0,4 |
2,8 |
2,7 |
2,5 |
0,8 |
–0,3 |
–0,1 |
1,4 |
|
2 |
0,3 |
4,5 |
2,5 |
–0,2 |
–0,1 |
–0,5 |
–0,9 |
–0,8 |
5,0 |
|||
|
3 |
0,2 |
5,3 |
2,5 |
–0,2 |
–0,1 |
–0,6 |
–1,0 |
–0,9 |
5,5 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Geoptimaliseerd uitgeborsteld beton |
70 |
80 |
1 |
–0,2 |
–0,7 |
1,4 |
1,2 |
1,1 |
–1,6 |
–2,0 |
–1,8 |
1,0 |
|
2 |
–0,7 |
3,0 |
–2,0 |
–1,4 |
–1,8 |
–2,7 |
–2,0 |
–1,9 |
–6,6 |
|||
|
3 |
–0,5 |
4,2 |
–1,9 |
–1,3 |
–1,7 |
–2,5 |
–1,8 |
–1,8 |
–6,6 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Fijn gebezemd beton |
70 |
120 |
1 |
8,0 |
–0,7 |
4,8 |
2,2 |
1,2 |
2,6 |
1,5 |
–0,6 |
7,6 |
|
2 |
0,2 |
8,6 |
7,1 |
3,2 |
3,6 |
3,1 |
0,7 |
0,1 |
3,2 |
|||
|
3 |
0,1 |
9,8 |
7,4 |
3,2 |
3,1 |
2,4 |
0,4 |
0,0 |
2,0 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Oppervlakte bewerking |
50 |
130 |
1 |
8,3 |
2,3 |
5,1 |
4,8 |
4,1 |
0,1 |
–1,0 |
–0,8 |
–0,3 |
|
2 |
0,1 |
6,3 |
5,8 |
1,8 |
–0,6 |
–2,0 |
–1,8 |
–1,6 |
1,7 |
|||
|
3 |
0,0 |
7,4 |
6,2 |
1,8 |
–0,7 |
–2,1 |
–1,9 |
–1,7 |
1,4 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Elementen- verharding in keper-verband |
30 |
60 |
1 |
27,0 |
16,2 |
14,7 |
6,1 |
3,0 |
–1,0 |
1,2 |
4,5 |
2,5 |
|
2 |
29,5 |
20,0 |
17,6 |
8,0 |
6,2 |
–1,0 |
3,1 |
5,2 |
2,5 |
|||
|
3 |
29,4 |
21,2 |
18,2 |
8,4 |
5,6 |
–1,0 |
3,0 |
5,8 |
2,5 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Elementen- verharding in dwars-verband |
30 |
60 |
1 |
31,4 |
19,7 |
16,8 |
8,4 |
7,2 |
3,3 |
7,8 |
9,1 |
2,9 |
|
2 |
34,0 |
23,6 |
19,8 |
10,5 |
11,7 |
8,2 |
12,2 |
10,0 |
2,9 |
|||
|
3 |
33,8 |
24,7 |
20,4 |
10,9 |
10,9 |
6,8 |
12,0 |
10,8 |
2,9 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Stille elementen- verharding |
30 |
60 |
1 |
26,8 |
13,7 |
11,9 |
3,9 |
–1,8 |
–5,8 |
–2,7 |
0,2 |
–1,7 |
|
2 |
9,2 |
5,7 |
4,8 |
2,3 |
4,4 |
5,1 |
5,4 |
0,9 |
0,0 |
|||
|
3 |
9,1 |
6,6 |
5,2 |
2,6 |
3,9 |
3,9 |
5,2 |
1,1 |
0,0 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Dunne deklagen A |
40 |
130 |
1 |
10,4 |
0,7 |
–0,6 |
–1,2 |
–3,0 |
–4,8 |
–3,4 |
–1,4 |
–2,9 |
|
2 |
13,8 |
5,4 |
3,9 |
–0,4 |
–1,8 |
–2,1 |
–0,7 |
–0,2 |
0,5 |
|||
|
3 |
14,1 |
6,1 |
4,1 |
–0,4 |
–1,8 |
–2,1 |
–0,7 |
–0,2 |
0,3 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|||
|
Dunne deklagen B |
40 |
130 |
1 |
6,8 |
–1,2 |
–1,2 |
–0,3 |
–4,9 |
–7,0 |
–4,8 |
–3,2 |
–1,8 |
|
2 |
13,8 |
5,4 |
3,9 |
–0,4 |
–1,8 |
–2,1 |
–0,7 |
–0,2 |
0,5 |
|||
|
3 |
14,1 |
6,1 |
4,1 |
–0,4 |
–1,8 |
–2,1 |
–0,7 |
–0,2 |
0,3 |
|||
|
4a/4b |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
Indeling van voertuigen
Definitie van voertuig en trein
Ten behoeve van deze berekeningsmethode voor geluidsbelasting wordt een voertuig gedefinieerd als een afzonderlijk deel van een trein (doorgaans een locomotief, zelf-aangedreven rijtuig, getrokken rijtuig of goederenwagon) dat onafhankelijk kan worden verplaatst en van de rest van de trein kan worden losgemaakt. Sommige specifieke omstandigheden kunnen optreden voor delen van een trein die deel uitmaken van een niet-afkoppelbare set, bijvoorbeeld die samen één draaistel delen. Ten behoeve van deze berekeningsmethode worden al deze delen in één voertuig samengebracht. Ten behoeve van deze berekeningsmethode bestaat een trein uit een reeks gekoppelde voertuigen.
Tabel 2.3.a1 definieert een gemeenschappelijke taal voor de beschrijving van de voertuigtypen die in de brondatabank zijn opgenomen. Zij geeft de relevante descriptoren die moeten worden gebruikt om de voertuigen in hun geheel te classificeren. Deze descriptoren stemmen overeen met de eigenschappen van het voertuig die invloed hebben op het akoestische richtingsafhankelijk geluidsvermogen per meter lengte van de equivalente gemodelleerde bronlijn.
Het aantal voertuigen per type wordt vastgesteld op elk van de baanvakken voor elk van de tijdsperioden die in de berekening van geluidsbelasting worden gebruikt. Het wordt uitgedrukt als een gemiddeld aantal voertuigen per uur, dat wordt verkregen door het totaal aantal voertuigen in een bepaalde periode te delen door de duur van deze periode in uren (bijvoorbeeld 24 voertuigen in vier uur betekent 6 voertuigen per uur). Alle voertuigtypen die op elk baanvak rijden, worden gebruikt.
|
Cijfer |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
|
Descriptor |
Voertuigtype |
Aantal assen per voertuig |
Type rem |
Wielmaatregel |
|
Verklaring van de descriptor |
Een letter die het type beschrijft |
Het werkelijk aantal assen |
Een letter die het type rem beschrijft |
Een letter die het type lawaaiverminderingsmaatregel beschrijft |
|
Mogelijke descriptoren |
h hogesnelheidsvoertuig (> 200 km/h) |
1 |
c gietijzeren blok |
n geen maatregel |
|
m zelf-aangedreven reizigersrijtuigen |
2 |
k blok van composietmetaal of sintermetaal |
d dempers |
|
|
p getrokken reizigersrijtuigen |
3 |
n niet op het loopvlak remmend, zoals schijf, trommel, magnetisch |
s schermen |
|
|
c stadstram of lichte metro zelf-aangedreven en niet-zelf-aangedreven rijtuig |
4 |
o overige |
||
|
d diesellocomotief |
enz |
|||
|
e elektrische locomotief |
||||
|
a algemeen vrachtvoertuig |
||||
|
o andere (dat wil zeggen onderhoudsvoertuigen enz.) |
In Nederland worden als voertuigtypen de voertuigcategorieën toegepast uit bijlage IV, paragraaf 1.2.1, bij het Reken- en meetvoorschrift geluid 2012, waarbij de descriptoren horen zoals aangegeven in tabel 2.3.a2.
|
Cat 1 |
m4cn |
|
Cat 2 |
m4cn, p4cn, m4nn, p4nn |
|
Cat 3 |
m4nn, p4nn, m4kn, p4kn |
|
Cat 4 |
a4cn |
|
Cat 5 |
d4cn |
|
Cat 6 |
d4nn |
|
Cat 7 |
c6nn |
|
Cat 8 |
m3nn, p3nn |
|
Cat 9 |
h3nn, h3kn, h3cn |
|
Cat 10 |
c3nn |
|
Cat 11 |
a4kn |
|
Cat 12 |
m2nn, m3nn |
Classificatie van railtypen
De bestaande railtypen kunnen verschillen, omdat verscheidene elementen bijdragen aan hun akoestische eigenschappen en deze karakteriseren. De railtypen die in deze methode worden gebruikt, staan vermeld in onderstaande tabel 2.3.b. Sommige elementen hebben een grote invloed op de akoestische eigenschappen, terwijl andere slechts een bijkomend effect hebben. In het algemeen zijn de meest relevante elementen die de emissie van het spoorweglawaai beïnvloeden: ruwheid van de railkop, stijfheid van de onderlegplaatjes, spoorbed, voegen en boogstraal. Als alternatief kunnen de algemene eigenschappen van het spoor worden gedefinieerd en in dit geval zijn de ruwheid van de railkop en de mate van afstandsdemping volgens ISO 3095 de meest essentiële akoestische parameters, plus de boogstraal.
Een baanvak wordt gedefinieerd als een deel van een enkel spoor, op een spoorlijn, station of depot, waarop de fysieke kenmerken en basiscomponenten van het spoor niet veranderen.
Tabel 2.3.b1 definieert een gemeenschappelijke taal voor de beschrijving van de railtypen die in de brondatabank zijn opgenomen.
|
Cijfer |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
Descriptor |
Spoorbed |
Ruwheid van de railkop |
Type onderleg-plaat |
Aanvullende maatregelen |
Voegen |
Boogstraal |
|
Verklaring van de descriptor |
Type spoorbed |
Indicator voor ruwheid |
Geeft een indicatie van de ‘dynamische’ stijfheid weer |
Een letter die de akoestische inrichting beschrijft |
Aanwezigheid van voegen en onderlinge afstand |
Geeft de boogstraal aan in m |
|
Toegestane codes |
B Ballast |
E Goed onderhouden en zeer glad |
S Zacht (150-250 MN/m) |
N Geen |
N Geen |
N Recht spoor |
|
S Betonplaten spoor |
M Normaal onderhouden |
M Gemiddeld (250 tot 800 MN/m) |
D Raildemper |
S Enkele voeg of wissel |
L Laag (1.000-500 m) |
|
|
L Brug volgestort met ballast |
N Niet goed onderhouden |
H Stijf (800-1.000 MN/m) |
B Minischerm |
D Twee voegen of wissels per 100 m |
M Gemiddeld (minder dan 500 m en meer dan 300 m) |
|
|
N Brug zonder ballast |
B Niet onderhouden en slechte conditie |
A Absorberende plaat op betonplaten- spoor |
M Meer dan twee voegen of wissels per 100 m |
H Hoog (minder dan 300 m) |
||
|
T Ingegoten spoor |
E Ingegoten spoorstaaf |
|||||
|
O Overige |
O Overige |
In Nederland worden als railtypen de bovenbouwconstructies toegepast uit bijlage IV, paragraaf 3.2, bij het Reken- en meetvoorschrift geluid 2012, waarbij de descriptoren horen zoals aangegeven in tabel 2.3.b2:
|
bb=1 |
BMHNNN |
|
bb=2 |
BMHNNN |
|
bb=3 |
BMHNSN, BMHNDN |
|
bb=4 |
SMHNNN |
|
bb=5 |
BMHNNN |
|
bb=6 |
SMMNNN/NMMNNN |
|
bb=7 |
BMMNNN |
|
bb=8 |
TM_ENN |
|
bb=9 |
SMHNNN |
|
bb=10 |
BMHDNN |
|
bb=11 |
OMHNNN |
|
bb=12 |
OMHDNN |
|
bb=1 |
BMHNDL |
|
bb=2 |
BMHNDL |
|
bb=3 |
BMHNDL |
|
bb=9 |
SMHNDL |
|
bb=11 |
OMHNDL |
Aantal en plaats van de equivalente geluidsbronnen
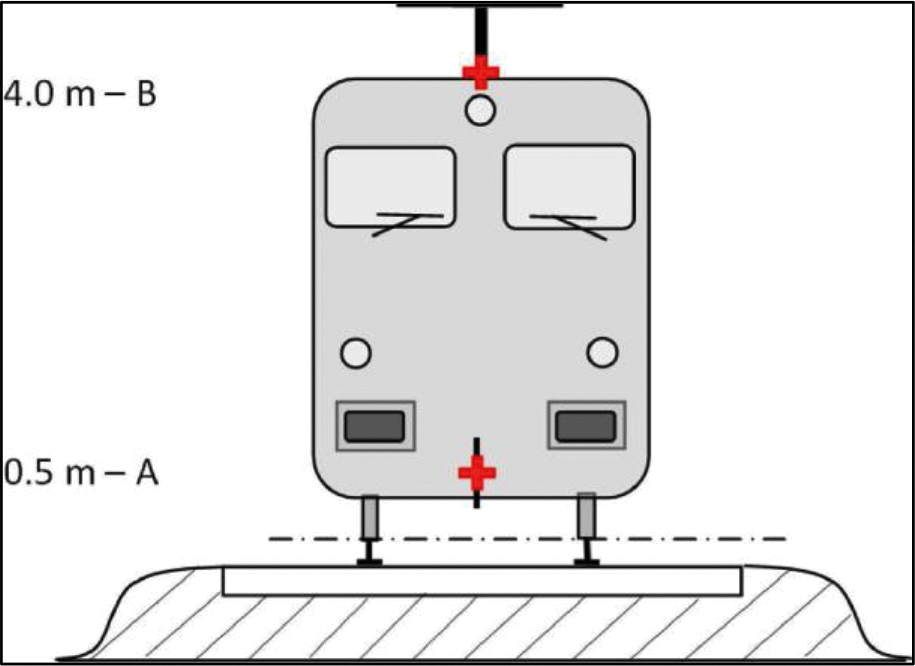
Figuur 2.3.a, Plaats van equivalente geluidsbronnen
De verschillende equivalente geluidsbronlijnen worden op verschillende hoogten en in het midden van het spoor geplaatst. Alle hoogten worden gerekend vanaf de raaklijn van de twee bovenste oppervlakken van de twee spoorstaven.
De equivalente bronnen omvatten verschillende fysieke bronnen (index p). Deze fysieke bronnen zijn onderverdeeld in verschillende categorieën, afhankelijk van het generatiemechanisme, en omvatten: 1) rolgeluid (waaronder niet alleen trillingen van rails en spoorbedding en wielen, maar ook, waar aanwezig, geluid van de wagenbovenbouw van de vrachtvoertuigen), 2) tractiegeluid, 3) aerodynamisch geluid, 4) stootgeluid (van overgangen, wissels en knooppunten), 5) booggeluid en 6) geluid door extra effecten zoals bruggen en viaducten.
1. De wiel- en railkopruwheid genereren langs drie transmissiepaden naar de afstralende oppervlakken (spoorstaven, wielen en bovenbouw), het rolgeluid. Dit wordt toegewezen aan h = 0,5 m (afstralende oppervlakken A) om de bijdrage van het spoor weer te geven, waaronder de invloed van het oppervlak van de spoorstaven, vooral betonplatenspoor (in overeenstemming met het voortplantende deel), om de bijdrage van de wielen weer te geven, en om de bijdrage van de wagenbovenbouw van het voertuig aan het geluid weer te geven (in goederentreinen).
2. De equivalente bronhoogten voor tractiegeluid variëren tussen 0,5 m (bron A) en 4,0 m (bron B), afhankelijk van de fysieke plaatsing van de component in kwestie. Bronnen zoals tandwieloverbrengingen en elektromotoren bevinden zich vaak op een ashoogte van 0,5 m (bron A). Louvres en koeleruitlaten kunnen zich op verschillende hoogten bevinden. Motoruitlaten voor dieselvoertuigen bevinden zich vaak op een dakhoogte van 4,0 m (bron B). Andere tractiebronnen zoals ventilatoren of dieselmotorblokken kunnen zich op een hoogte van 0,5 m (bron A) of 4,0 m (bron B) bevinden. Als de exacte bronhoogte zich tussen de modelhoogten bevindt, wordt de geluidsenergie proportioneel over de dichtstbijzijnde aangrenzende bronhoogten verdeeld. Om deze reden voorziet de methode twee bronhoogten op 0,5 m (bron A) en 4,0 m (bron B) en wordt het equivalente geluidsvermogen van beide tussen de twee verdeeld, afhankelijk van de specifieke configuratie van de bronnen op het type eenheid.
3. Aerodynamische geluidseffecten houden verband met de bron op 0,5 m (mantels en schermen, bron A) en de bron op 4,0 m (alle inrichtingen op het dak en de stroomafnemer, bron B). De keuze van 4,0 m voor de effecten van de stroomafnemer staat bekend als een eenvoudig model, en moet zorgvuldig worden overwogen als het doel de keuze van een correcte hoogte voor geluidsschermen is.
4. Stootgeluid houdt verband met de bron op 0,5 m (bron A).
5. Booggeluid houdt verband met de bronnen op 0,5 m (bron A).
6. Bruggeluid houdt verband met de bron op 0,5 m (bron A).
Algemene vergelijking
Individueel voertuig
Het model voor spoorweglawaai, dat analoog is aan wegverkeerslawaai, beschrijft de geluidsvermogensemissie van een specifieke combinatie van voertuigtype en spoortype die aan een aantal eisen voldoet die in de voertuig- en spoorclassificatie zijn beschreven, uitgedrukt in een reeks geluidsvermogens voor elk voertuig (LW,0).
Verkeersstroom
De geluidsemissie van een verkeersstroom op elk spoor wordt weergegeven met een set van twee bronlijnen die zijn gekenmerkt door hun gerichte geluidsvermogen per meter per frequentieband. Dit komt overeen met de som van de geluidsemissies als gevolg van de afzonderlijke voertuigen die in de verkeersstroom passeren en houdt, in het specifieke geval van stilstaande voertuigen, rekening met de tijd die de voertuigen in het baanvak in kwestie verblijven.
Het richtingsafhankelijke geluidsvermogen per meter per frequentieband, als gevolg van alle voertuigen die elk baanvak op het spoortype (j) passeren, wordt gedefinieerd:
• voor elke frequentieband (i)
• voor elk gegeven bronhoogte (h) (voor bronnen op 0,5 m h = 1, op 4,0 m h = 2), en is de energiesom van alle bijdragen van alle voertuigen die op het specifieke baanvak (j) rijden.
Deze bijdragen zijn:
• van alle voertuigentypen (t)
• op verschillende snelheden (s)
• onder de specifieke rijcondities (constante snelheid) (c)
• voor elk fysiek brontype (rollen, contact, booggeluid, tractie, aerodynamische en overige bronnen, zoals bruggeluid) (p).
Voor de berekening van het gerichte geluidsvermogen per meter (invoer in het voortplantende deel) als gevolg van de gemiddelde mix van verkeer op het baanvak (j), wordt het volgende gebruikt:
|
|
(2.3.1) |
waarbij
• Tref de referentieperiode waarvoor het gemiddelde verkeer wordt beschouwd is;
• x het totaal aantal bestaande combinaties van i, t, s, c, p voor elk j-de baanvak is;
• t de index voor voertuigtypen op het j-de baanvak is;
• s de index voor de treinsnelheid is: er zijn net zo veel indexen als het aantal verschillende gemiddelde treinsnelheden op het j-de baanvak;
• c de index voor rijcondities is: 1 (voor constante snelheid), 2 (stationair draaien);
• p de index voor de fysieke brontypen is: 1 (voor rol- en stootgeluid), 2 (booggeluid), 3 (tractiegeluid), 4 (aerodynamisch geluid), 5 (overige bronnen);
• Lw’,eq,lijn,x x-de richtingsafhankelijke geluidsvermogen is per meter voor een bronlijn van één combinatie van t, s, c, p op elk j-de baanvak.
Als wordt uitgegaan van een constante stroom van Q voertuigen per uur, met een gemiddelde snelheid ν, dan is er gemiddeld op elk tijdstip een equivalent aantal Q/ν voertuigen per lengte-eenheid van het baanvak. De geluidsemissie van de voertuigstroom uitgedrukt in richtingsafhankelijke geluidsvermogen per meter Lw’,eq,lijn uitgedrukt in dB/m (re. 10-12 W) wordt geïntegreerd door:
|
|
(2.3.2) |
waarbij
• Q het gemiddelde aantal voertuigen per uur op het j-de baanvak voor voertuigtype t, gemiddelde treinsnelheid s en rijconditie c is,
• ν hun snelheid [km/h] op het j-de baanvak voor voertuigtype t en gemiddelde treinsnelheid s is,
• LW,0,dir het niveau van het richtingsafhankelijke geluidsvermogen is van het specifieke geluid (rol-, stoot-, boog-, rem-, tractie-, aerodynamisch geluid en geluid van andere bronnen) van een enkel voertuig in de richtingen Ψ,φ gedefinieerd met betrekking tot de bewegingsrichting van het voertuig (zie figuur 2.3.b).
Bij een stationaire bron, net als tijdens stationair draaien, wordt ervan uitgegaan dat het voertuig gedurende een totale tijd Tidle op een locatie binnen een baanvak met lengte L blijft. Dat betekent dat met Tref als de referentieperiode voor de beoordeling van geluidsbelasting (bijvoorbeeld 12 uur, 4 uur, 8 uur), het richtingsafhankelijk geluidsvermogen per lengte eenheid op dat baanvak wordt bepaald door:
|
|
(2.3.3) |
In het algemeen wordt gericht geluidsvermogen uit elke specifieke bron verkregen als:
|
LW,0,dir,i (Ψ, φ) = LW,0 + ∆LW,dir,vert,i + ∆LW,dir,hor,i |
(2.3.4) |
waarbij
• ∆LW,dir,vert,i de correctiefunctie is voor verticaal richteffect (dimensieloos) van Ψ (figuur 2.3.b)
• ∆LW,dir,hor,i de correctiefunctie is voor horizontaal richteffect (dimensieloos) van φ (figuur 2.3.b)
• LW,0,dir,i
(Ψ,φ), afgeleid in 1/3-octaafbanden, wordt uitgedrukt in
octaafbanden door elke bijbehorende 1/3-octaafband energetisch in de
overeenkomstige octaafband toe te voegen.
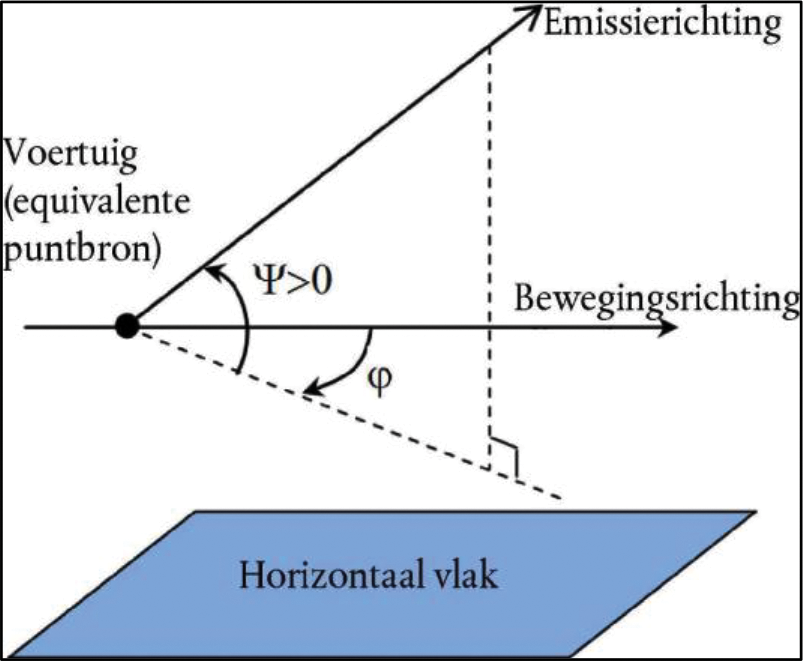
Figuur 2.3.b, Geometrische definitie
Ten behoeve van de berekeningen wordt de bronsterkte vervolgens specifiek uitgedrukt in richtingsafhankelijk geluidsvermogen per 1 m spoorlengte LW’,tot,dir,i om het richteffect van de bronnen in hun verticale en horizontale richting in aanmerking te nemen door middel van aanvullende correcties.
Verscheidene LW,0,dir,i (Ψ,φ) worden voor elke combinatie van voertuig-spoor-snelheid-rijconditie beschouwd:
• voor een 1/3-octaafbandfrequentie (i),
• voor elk baanvak (j),
• bronhoogte (h) (voor bronnen op 0,5 m h = 1, op 4,0 m h = 2),
• richteffect (d) van de bron.
Een reeks LW,0,dir,i (Ψ,φ) wordt beschouwd voor elke combinatie van voertuig-spoor-snelheid-rijconditie, elk baanvak, de hoogten die met h = 1 en h = 2 overeenstemmen, en het richteffect.
Rolgeluid
De bijdragen van het voertuig en het spoor aan rolgeluid worden in vier essentiële elementen verdeeld: wielruwheid, railruwheid, voertuigoverdrachtsfunctie naar de wielen en de wagenbovenbouw (voertuigen) en de spooroverdrachtsfunctie. Wiel- en railruwheid geven de oorzaak van de excitatie van de trilling op het contactpunt tussen rail en wiel weer. De overdrachtsfuncties zijn twee empirische of gemodelleerde functies die alle complexe verschijnselen van de generatie van mechanische trilling en geluid op de oppervlakken van de wielen, rails, dwarsliggers en onderbouw van het spoor weergeven. Deze verdeling stemt overeen met het fysieke bewijs dat ruwheid op een rail de trilling van de rail kan exciteren, maar ook de trilling van het wiel zal exciteren en omgekeerd. Het niet opnemen van een van deze vier parameters zou het ontkoppelen van de classificatie van sporen en treinen verhinderen.
Wiel en railruwheid
Rolgeluid wordt voornamelijk door de rail- en wielruwheid in het golflengtegebied van 5-500 mm geëxciteerd.
Definitie
Het ruwheidsniveau Lr wordt gedefinieerd als tienmaal de logaritme met grondgetal 10 van de kwadratisch gemiddelde waarde r2 van de ruwheid van het loopvlak van een rail of wiel in de bewegingsrichting (longitudinaal niveau), gemeten in μm over een bepaalde raillengte of de gehele wieldiameter, gedeeld door het kwadraat van de referentiewaarde r02:
|
|
(2.3.5) |
waarbij
r0 = 1 μm
r = kwadratisch gemiddelde van het verschil van de verticale verplaatsing van het contactoppervlak naar het gemiddelde niveau.
Het ruwheidsniveau Lr wordt gewoonlijk verkregen als een spectrum van golflengte λ en wordt geconverteerd naar een frequentiespectrum f = ν/λ, waarbij f de middenfrequentie van een bepaalde 1/3-octaafband in Hz, λ de golflengte in m, en ν de treinsnelheid in m/s is. Het ruwheidsspectrum als een functie van frequentie verschuift langs de frequentie-as voor verschillende snelheden. In algemene gevallen dienen na conversie naar het frequentiespectrum door middel van de snelheid, nieuwe waarden voor 1/3-octaafbandspectra te worden verkregen met gemiddelden die tussen twee overeenstemmende 1/3-octaafbanden in het golflengtedomein liggen. Om het frequentiespectrum van de totale effectieve ruwheid te schatten dat met de relevante treinsnelheid overeenkomt, wordt het gemiddelde van de twee overeenkomstige, in het golflengtedomein gedefinieerde, 1/3-octaafbanden energetisch en proportioneel berekend.
De railruwheid (ruwheid van de kant van het spoor) voor het golfgetal (i) wordt gedefinieerd als Lr,TR,i
Overeenkomstig wordt de wielruwheid (ruwheid van de kant van het voertuig) voor het golfgetal (i) gedefinieerd als Lr,VEH,i
De totale en effectieve ruwheid voor golfgetal i (LR,TOT,i) wordt gedefinieerd als de energetische som van de ruwheid van de rail en die van het wiel, vermeerderd met het A3(λ) contactfilter om de filterende werking van de contactplaats tussen de spoorstaaf en het wiel in aanmerking te nemen, en is in dB:
|
|
(2.3.6) |
waar het wordt uitgedrukt als een functie van het i-de golfgetal dat overeenkomt met de golflengte λ. Het contactfilter is afhankelijk van het rail- en wieltype en de belasting.
De totale effectieve ruwheid voor het j-de baanvak en elk t-de voertuigtype op de overeenkomstige snelheid ν, wordt in de methode gebruikt.
Overdrachtsfunctie van voertuig, spoor en wagenbovenbouw
Drie snelheidsonafhankelijke overdrachtsfuncties, LH,TR,i, LH,VEH,i en LH,VEH,SUP,i, worden gedefinieerd: de eerste voor elk j-de baanvak en de twee volgende voor elk t-de voertuigtype. Zij relateren de totale effectieve ruwheid aan het geluidsvermogen van respectievelijk het spoor, de wielen en de wagenbovenbouw.
De bijdrage van de wagenbovenbouw wordt alleen voor goederenwagons in aanmerking genomen, dus alleen voor voertuigtype ‘a’.
Daardoor worden voor rolgeluid de bijdragen van het spoor en van het voertuig volledig beschreven door deze overdrachtsfuncties en de totale effectieve ruwheid. Bij stationair draaien van een trein wordt rolgeluid uitgesloten.
Voor geluidsvermogen per voertuig wordt het rolgeluid op ashoogte berekend, en heeft dit als invoer de totale effectieve ruwheid LR,TOT,i als functie van de voertuigsnelheid ν, de overdrachtsfuncties van het spoor, het voertuig en de wagenbovenbouw LH,TR,i, LH,VEH,i en LH,VEH,SUP,i, en het totale aantal assen Na:
voor h =1:
|
LW,0,TR,i = LR,TOT,i + LH,TR,i + 10lg(Na) |
(2.3.7) |
|
LW,0,VEH,i = LR,TOT,i + LH,VEH,i + 10lg(Na) |
(2.3.8) |
|
LW,0,VEHSUP,i = LR,TOT,i + LH,VEHSUP,i + 10lg(Na) |
(2.3.9) |
waarbij Na het aantal assen per
voertuig voor het t-de voertuigtype is.
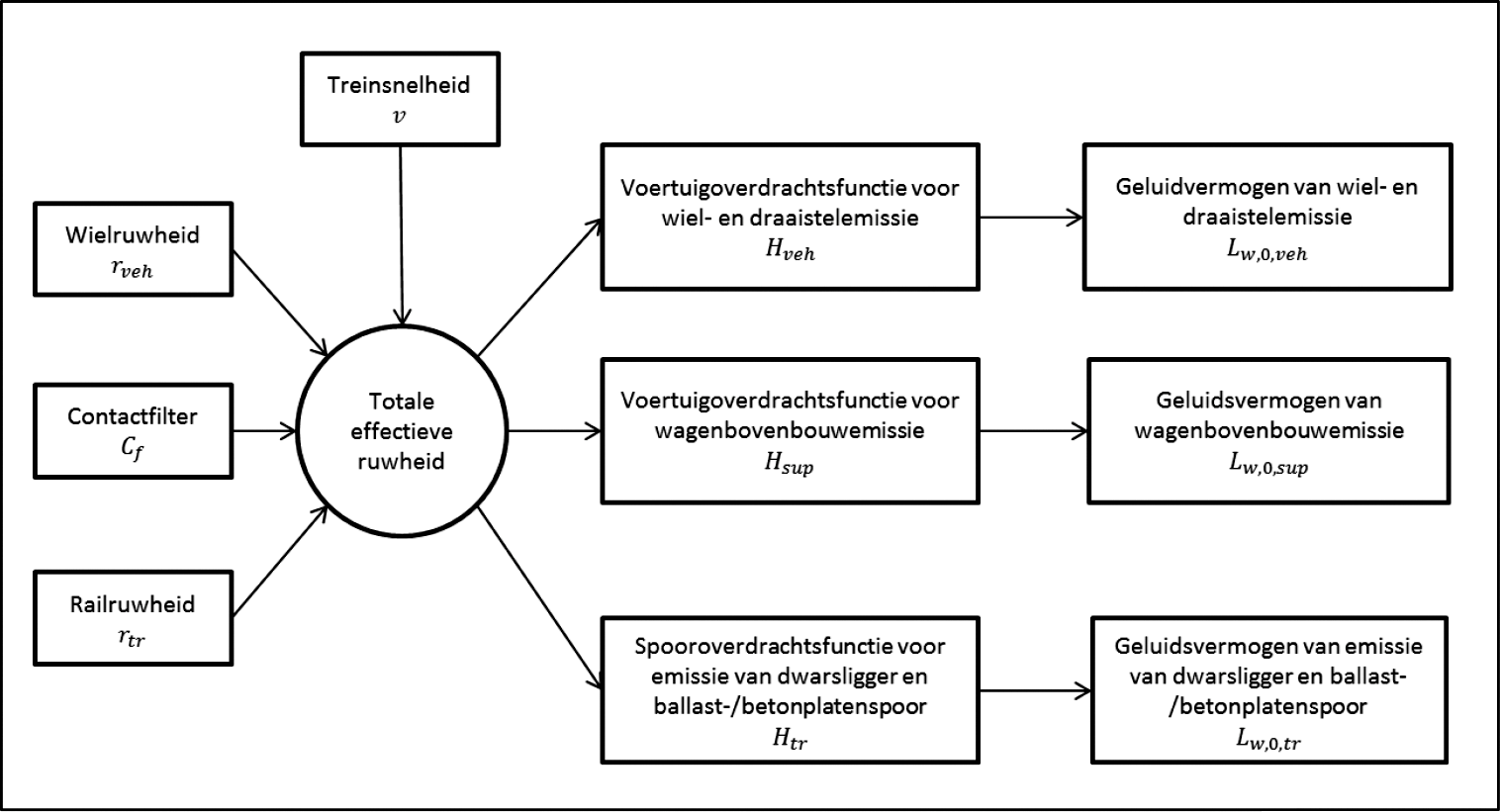
Figuur 2.3.c, Regeling van het gebruik van de verschillende definities van ruwheid en overdrachtsfunctie
Een minimumsnelheid van 50 km/h (30 km/h alleen voor trams en lichte metro) wordt gebruikt om de totale effectieve ruwheid en dus het geluidsvermogen van de voertuigen te bepalen (deze snelheid heeft geen invloed op de berekening van de voertuigstroom) ter compensatie van de potentiële fout als gevolg van de vereenvoudiging van de definitie van rolgeluid, van remgeluid en van stootgeluid van overgangen en wissels.
Stootgeluid (overgangen, wissels en knooppunten)
Stootgeluid kan worden veroorzaakt door overgangen, wissels en voegen of puntstukken. Het kan variëren in grootte en kan rolgeluid overheersen. Stootgeluid wordt voor sporen met uitzetvoegen in aanmerking genomen. Voor stootgeluid door wissels, overgangen en voegen in baanvakken op een snelheid van minder dan 50 km/h (30 km/h voor trams en lichte metro) wordt modellering vermeden, omdat de minimumsnelheid van 50 km/h (30 km/h voor trams en lichte metro) wordt gebruikt om meer effecten op te nemen in overeenstemming met de beschrijving van het hoofdstuk over rolgeluid. Daarnaast wordt modellering van stootgeluid ook onder rijconditie c = 2 (stationair draaien) vermeden.
Stootgeluid wordt in de term rolgeluid opgenomen door een aanvullende fictieve contactruwheid (energetisch) toe te voegen aan de totale effectieve ruwheid op elk specifiek j-de baanvak waar dit aanwezig is. In dit geval wordt een nieuw LR,TOT+IMPACT,i in plaats van LR,TOT,i gebruikt en wordt dan:
|
|
(2.3.10) |
LR,IMPACT,i is een 1/3-octaafbandspectrum (als een functie van frequentie). Om dit frequentiespectrum te verkrijgen, wordt een spectrum als een functie van golflengte λ gegeven en naar het gewenste spectrum als een functie van frequentie geconverteerd met behulp van de verhouding λ = ν/f, waarbij f de middenfrequentie van de 1/3-octaafband in Hz en ν de s-de voertuigsnelheid van het t-de voertuigtype in m/s is.
Stootgeluid hangt af van het aantal en de hardheid van de contacten per lengte-eenheid of voegdichtheid, dus in het geval waar meerdere contacten worden gegeven, wordt de impactruwheid die in de bovenstaande vergelijking wordt gebruikt als volgt berekend:
|
|
(2.3.11) |
waarbij LR,IMPACT-SINGLE,i de contactruwheid zoals gegeven voor een enkel contact is en nl de lasdichtheid is.
Het standaardniveau van contactruwheid wordt voor een voegdichtheid nl = 0,01 m-1 gegeven, ofwel één voeg per elke 100 m spoor. Situaties met verschillende aantallen voegen worden benaderd door de dichtheid van het aantal lassen nlaan te passen. Opgemerkt wordt dat bij de modellering van de spoorligging en segmentatie, de dichtheid van het aantal voegen in aanmerking wordt genomen, dat wil zeggen het kan nodig zijn om een afzonderlijk bronsegment voor een stuk spoor met meer voegen te gebruiken. De LW,0 van de bijdragen van het spoor, wiel/draaistel en de wagenbovenbouw wordt door middel van de LR,IMPACT,i voor +/- 50 m vóór en na de spoorstaaflas verhoogd. Bij een reeks voegen wordt de verhoging uitgebreid naar tussen – 50 m vóór de eerste voeg en + 50 m na de laatste voeg.
De toepasbaarheid van deze geluidsvermogensspectra wordt normaliter ter plaatse gecontroleerd. Voor gelaste sporen wordt een standaard nl van 0,01 gebruikt.
Booggeluid
Booggeluid is een bijzondere bron die alleen relevant is voor bogen en is daarom een lokaal effect. Booggeluid hangt in het algemeen af van boogkromming, wrijvingscondities, treinsnelheid, rail-wielgeometrie en -dynamiek. Omdat het aanzienlijk kan zijn, is een passende beschrijving vereist. Op locaties waar booggeluid optreedt, meestal in bogen en wisselbogen (in afbuigende richting bereden), moeten geschikte spectra voor overtollig geluidsvermogen worden toegevoegd aan het bronvermogen. De geluidtoeslag kan specifiek zijn voor elk type rollend materieel, aangezien bepaalde wiel- en draaisteltypen aanzienlijk minder gevoelig zijn voor booggeluid dan andere. Als er metingen van de geluidtoeslag beschikbaar zijn die voldoende rekening houden met het stochastische karakter van het booggeluid, kunnen deze worden gebruikt.
Als er geen geschikte metingen beschikbaar zijn, kan een eenvoudige benadering worden gevolgd. Bij deze benadering wordt het booggeluid in aanmerking genomen door de volgende toeslagen aan de geluidsvermogensspectra van rolgeluid voor alle frequenties toe te voegen.
|
Trein |
5 dB voor bogen met 300 m < R ≤ 500 m en ltrack ≥ 50 m 8 dB voor bogen met R ≤ 300 m en ltrack ≥ 50 m 8 dB voor wisselbogen met R ≤ 300 m 0 dB anders |
|
Tram |
5 dB voor bogen en wisselbogen met R ≤ 200 m 0dB anders |
waarbij ltrack de lengte van het spoor langs de boog is en R de straal van de boog.
De toepasbaarheid van deze geluidsvermogensspectra of overtollige waarden wordt normaal gesproken ter plaatse gecontroleerd, met name voor trams en voor locaties waar bogen of wisselbogen worden behandeld met maatregelen tegen booggeluid.
Tractiegeluid
Hoewel tractiegeluid in het algemeen eigen is aan elke kenmerkende bedrijfsconditie, waaronder constante snelheid, vertragen, versnellen en stationair draaien, zijn de enige twee gemodelleerde condities constante snelheid (dat geldt ook wanneer de trein vertraagt of versnelt) en stationair draaien. De gemodelleerde bronsterkte komt alleen overeen met maximale belasting en dit leidt tot de hoeveelheden LW,0,const,i = LW,0,idling,i. Bovendien stemt LW,0,idling,i overeen met de bijdrage van alle fysieke bronnen van een bepaald voertuig die toe te schrijven is aan een bepaalde hoogte, zoals beschreven in 2.3.1.
LW,0,idling,i wordt uitgedrukt als een statische geluidsbron bij stationair draaien voor de duur van de stationaire toestand, en wordt gebruikt als een model van een vaste puntbron zoals beschreven in het volgende hoofdstuk over industrielawaai. Dit wordt alleen in aanmerking genomen indien treinen langer dan 0,5 uur stationair draaien.
Deze hoeveelheden kunnen van metingen van alle bronnen bij elke bedrijfsconditie worden verkregen, of de gedeeltelijke bronnen kunnen afzonderlijk worden aangemerkt om hun parameterafhankelijkheid en de relatieve sterkte te bepalen. Dit kan door middel van metingen op een stationair voertuig worden gedaan door assnelheden van de tractie-uitrusting te variëren, in navolging van ISO 3095:2005. Voor zover relevant moeten meerdere tractiegeluidsbronnen worden gekenmerkt die mogelijk niet alle van de treinsnelheid afhankelijk zijn:
• geluid van de aandrijflijn, zoals dieselmotoren (waaronder inlaat, uitlaat en motorblok), tandwieltransmissie, elektrische generatoren, grotendeels afhankelijk van het toerental van de motor (omw./min.), en elektrische bronnen zoals omvormers, die voornamelijk van de lading afhankelijk kunnen zijn;
• geluid van ventilatoren en koelsystemen, afhankelijk van het toerental van de ventilator. In sommige gevallen kunnen ventilatoren rechtstreeks aan de aandrijflijn worden gekoppeld;
• periodieke bronnen zoals compressoren, kleppen en andere met een karakteristieke bedrijfsduur en overeenkomstige bedrijfscycluscorrectie voor de geluidsemissie.
Omdat elk van deze bronnen zich bij elke bedrijfsconditie anders kan gedragen, wordt het tractiegeluid dienovereenkomstig gespecificeerd. De bronsterkte wordt verkregen van metingen onder gecontroleerde omstandigheden. In het algemeen vertonen locomotieven meer variatie in belasting, omdat het aantal voertuigen dat wordt getrokken, en daardoor het uitgangsvermogen, aanzienlijk kan variëren, terwijl de vaste treinsamenstellingen zoals met elektrische motoren aangedreven meervoudige eenheden (EMU's), dieseltreinstellen (DMU's) en hogesnelheidstreinen een beter gedefinieerde belasting hebben.
Er is geen a priori toewijzing van het brongeluidsvermogen aan de bronhoogte, en deze keuze hangt af van de beoordeling van het specifieke geluid en specifieke voertuig. Het wordt gemodelleerd om zich op bron A (h = 1) en bron B (h = 2) te bevinden.
Aerodynamisch geluid
Aerodynamisch geluid is alleen relevant op hoge snelheden van meer dan 200 km/h. Daarom moet eerst worden nagegaan of het voor de toepassingsdoeleinden werkelijk noodzakelijk is. Als de functies rolgeluid, ruwheid en overdracht bekend zijn, kan het naar hogere snelheden worden geëxtrapoleerd en kan een vergelijking worden gemaakt met bestaande gegevens van hogesnelheidslijnen om na te gaan of aerodynamisch geluid hogere niveaus oplevert. Als de treinsnelheden op een netwerk hoger dan 200 km/h maar niet meer dan 250 km/h zijn, is het in sommige gevallen niet nodig om aerodynamisch geluid ook op te nemen, afhankelijk van het voertuigontwerp.
De bijdrage van aerodynamisch geluid wordt gegeven als een functie van snelheid:
|
|
(2.3.12) |
|
|
(2.3.13) |
waarbij
ν0 een snelheid is waarop aerodynamisch geluid dominant is en op 300 km/h is vastgesteld,
LW,0,1,i een referentiegeluidsvermogen is dat wordt bepaald op basis van twee of meer meetpunten voor bronnen op een bekende bronhoogte, bijvoorbeeld op het eerste draaistel,
LW,0,2,i een referentiegeluidsvermogen is dat wordt bepaald op basis van twee of meer meetpunten voor bronnen op een bekende bronhoogte, bijvoorbeeld de hoogte van de uitsparing van de stroomafnemer,
α1,i een coëfficiënt is die wordt bepaald op basis van twee of meer meetpunten voor bronnen op een bekende bronhoogte, bijvoorbeeld op het eerste draaistel,
α2,i een coëfficiënt is die wordt bepaald op basis van twee of meer meetpunten voor bronnen op een bekende bronhoogte, bijvoorbeeld de hoogte van de uitsparing van de stroomafnemer.
Richteffect van de bron
Het horizontale richteffect ∆LW,dir,hor,i in dB wordt in het horizontale vlak gegeven en kan als standaard worden aangenomen een dipool te zijn voor rolgeluid, stootgeluid (voegen enz.), booggeluid, remmen, ventilatoren en aerodynamische effecten, en wordt voor elke i-de frequentieband als volgt berekend:
|
∆LW,dir,hor,i = 10lg (0,01 + 0,99 * sin2φ) |
(2.3.14) |
Bruggeluid wordt gemodelleerd bij bron A (h=1), waarbij wordt uitgegaan van omni-directionaliteit.
Het verticale richteffect ∆LW,dir,ver,i in dB wordt in het verticale vlak gegeven voor bron A (h=1), als een functie van de middenfrequentie fc,i van elke i-de frequentieband, en:
voor 0 < ψ < π/2 is
|
|
(2.3.15) |
voor – π/2 < ψ < 0 is
ΔLW,dir,ver,i = 0
Voor bron (h = 2) voor het aerodynamisch effect:
|
ΔLW,dir,ver,i = 10lg (cos2 (ψ)) voor ψ<0 LW,dir,ver,i = 0 elders |
(2.3.16) |
Richteffect ∆LW,dir,ver,i wordt niet in aanmerking genomen voor bron B (h = 2) voor overige geluidbronnen, omdat voor deze bronnen in deze positie omnidirectionaliteit wordt aangenomen.
Correctie voor geluid van kunstwerken (bruggen en viaducten)
In het geval dat het baanvak zich op een brug bevindt, is het noodzakelijk om het extra geluid dat wordt geproduceerd door de trilling van de brug als gevolg van de excitatie die door de aanwezigheid van de trein wordt veroorzaakt, in aanmerking te nemen. Het bruggeluid is gemodelleerd als een extra bron waarvan het geluidsvermogen per voertuig wordt verkregen door
|
ΔLW,0,bridge,i = LR,TOT,i + LH,bridge,i +10lg (Na) |
(2.3.17) |
waarbij LH,bridge,i de brugoverdrachtsfunctie is. Het bruggeluid ∆LW,0,bridge,i vertegenwoordigt alleen het geluid dat door de structuur van de brug wordt uitgestraald. Het rolgeluid van een voertuig op de brug wordt berekend met behulp van de formules 2.3.8 tot en met 2.3.10, door de spooroverdrachtsfunctie te kiezen die overeenkomt met het spoorsysteem dat op de brug aanwezig is. Er wordt over het algemeen geen rekening gehouden met geluidschermen of obstakels aan de randen van de brug.
Correctie voor andere spoorgerelateerde geluidsbronnen
Diverse bronnen zoals opslagplaatsen, laad- en losplaatsen, stations, bellen, stationsluidsprekers enz., kunnen aanwezig zijn en houden verband met het spoorgeluid. Deze bronnen worden als bronnen van industrielawaai (vaste geluidsbronnen) behandeld en, indien van toepassing, overeenkomstig het volgende hoofdstuk over industrielawaai gemodelleerd.
|
Parameter |
Parameters |
|---|---|
|
Spooroverdrachtsfunctie |
LH,TR |
|
Voertuigoverdrachtsfunctie |
LH,VEH |
|
Wagenopbouw-overdrachtsfunctie |
LH,VEH,SUP |
|
Brugoverdrachtsfunctie |
LH,bridge |
|
Tractiegeluid |
LW,0,idling |
|
Aerodynamisch geluid |
α1, LW,0,1, α2, LW,0,2 |
|
Railruwheid |
Lr,TR |
|
Wielruwheid |
Lr,VEH |
|
Stootgeluid (voegruwheid) |
LR,IMPACT |
|
Contactfilter |
A3 |
|
Frequentie [Hz] |
bb=1 ‘mono | medium’ |
bb=2 |
bb=3 |
bb=4 |
bb=5 |
bb=6 |
bb=7 |
bb=8 |
bb=9 |
bb=10 |
bb=11 |
bb=12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
50 |
50,9 |
69,6 |
Neem ‘mono |Medium’ en pas ‘Impact Noise’ toe. Zie tabel 2.3.e voor de nl waarde en zie tabel 2.3.h voor de voegruwheid ‘NL’. |
80,2 |
80,2 |
75,4 |
80,2 |
78,8 |
81,5 |
50,9 |
50,9 |
50,9 |
|
63 |
57,8 |
71,7 |
82,1 |
82,1 |
77,4 |
82,1 |
80,7 |
83,4 |
57,8 |
57,8 |
57,8 |
|
|
80 |
66,5 |
75,9 |
86,0 |
86,0 |
81,4 |
86,0 |
84,7 |
87,3 |
66,5 |
66,5 |
66,5 |
|
|
100 |
76,8 |
81,0 |
92,2 |
92,2 |
87,1 |
81,0 |
87,1 |
83,5 |
76,8 |
76,8 |
76,8 |
|
|
125 |
80,9 |
83,2 |
92,8 |
92,8 |
88,0 |
83,2 |
88,0 |
85,1 |
80,9 |
80,9 |
80,9 |
|
|
160 |
83,3 |
85,3 |
94,4 |
94,4 |
89,7 |
85,3 |
89,7 |
87,0 |
83,3 |
83,3 |
83,3 |
|
|
200 |
85,8 |
87,6 |
95,4 |
96,5 |
83,4 |
85,8 |
90,6 |
87,6 |
83,4 |
85,8 |
83,8 |
|
|
250 |
90,0 |
91,8 |
99,6 |
100,7 |
87,7 |
90,0 |
94,8 |
91,8 |
87,7 |
90,0 |
88,0 |
|
|
315 |
91,6 |
93,2 |
100,4 |
101,5 |
89,8 |
91,6 |
95,8 |
93,2 |
89,8 |
91,6 |
89,6 |
|
|
400 |
93,9 |
99,8 |
105,0 |
104,0 |
97,5 |
93,9 |
100,8 |
98,7 |
90,0 |
100,9 |
97,9 |
|
|
500 |
95,6 |
101,2 |
106,3 |
105,3 |
99,0 |
95,6 |
102,2 |
100,1 |
91,0 |
102,6 |
99,6 |
|
|
630 |
97,4 |
103,0 |
108,1 |
107,1 |
100,8 |
97,4 |
104,0 |
101,9 |
92,0 |
104,4 |
101,4 |
|
|
800 |
101,7 |
103,9 |
110,1 |
103,9 |
104,9 |
101,7 |
103,9 |
109,1 |
94,0 |
108,7 |
106,7 |
|
|
1.000 |
104,4 |
106,6 |
112,8 |
106,6 |
111,8 |
104,4 |
106,6 |
111,8 |
96,0 |
111,4 |
109,4 |
|
|
1.250 |
106,0 |
108,4 |
114,9 |
108,4 |
113,9 |
106,0 |
108,4 |
113,9 |
97,0 |
113,0 |
111,0 |
|
|
1.600 |
106,8 |
108,3 |
113,3 |
108,3 |
115,5 |
106,8 |
108,3 |
117,6 |
97,0 |
109,8 |
101,8 |
|
|
2.000 |
108,3 |
110,4 |
116,1 |
110,4 |
114,9 |
108,3 |
110,4 |
120,7 |
98,0 |
111,3 |
103,3 |
|
|
2.500 |
108,9 |
112,5 |
119,6 |
112,5 |
118,2 |
108,9 |
112,5 |
124,4 |
98,0 |
111,9 |
103,9 |
|
|
3.150 |
109,1 |
112,7 |
118,3 |
112,7 |
118,3 |
109,1 |
109,1 |
119,7 |
97,0 |
111,1 |
106,1 |
|
|
4.000 |
109,4 |
112,8 |
118,4 |
112,8 |
118,4 |
109,4 |
109,4 |
119,8 |
96,0 |
111,4 |
106,4 |
|
|
5.000 |
109,9 |
113,3 |
118,9 |
113,3 |
118,9 |
109,9 |
109,9 |
120,3 |
95,0 |
111,9 |
106,9 |
|
|
6.300 |
109,9 |
113,4 |
109,9 |
113,4 |
117,5 |
109,9 |
109,9 |
113,4 |
94,7 |
109,9 |
105,9 |
|
|
8.000 |
110,3 |
113,8 |
110,3 |
113,8 |
117,9 |
110,3 |
110,3 |
113,8 |
95,1 |
110,3 |
106,3 |
|
|
10.000 |
111,0 |
114,5 |
111,0 |
114,5 |
118,6 |
111,0 |
111,0 |
114,5 |
95,8 |
111,0 |
107,0 |
|
Bb |
m |
Spoor |
LR,IMPACT |
nl |
|---|---|---|---|---|
|
<>3 |
1 |
Voegloos |
Leeg |
0,01 (of nvt) |
|
3 |
2 |
Voegenspoor (1 per 30 m) |
‘NL’ (Tabel 2.3.h) |
0,033 |
|
3 |
3 |
intern-voegloos wissel (1/lengte) |
‘NL’ (Tabel 2.3.h) |
1/wissellengte |
|
3 |
4 |
niet-voegloos wissel (3/lengte) |
‘NL’ (Tabel 2.3.h) |
3/wissellengte |
|
Frequentie [Hz] |
In ballast ‘duo | medium’ |
Grasbaan |
In asfalt |
Trambaan-platen |
In klinkers met Ortec klemplaat |
|---|---|---|---|---|---|
|
50 |
50,0 |
83,4 |
76,9 |
82,5 |
77,2 |
|
63 |
56,1 |
85,3 |
78,8 |
84,5 |
79,1 |
|
80 |
64,1 |
89,2 |
82,7 |
88,3 |
83,0 |
|
100 |
72,5 |
88,4 |
74,8 |
84,8 |
85,4 |
|
125 |
75,8 |
87,8 |
73,6 |
84,4 |
84,9 |
|
160 |
79,1 |
89,1 |
77,9 |
85,9 |
86,4 |
|
200 |
83,6 |
87,9 |
88,3 |
85,5 |
83,6 |
|
250 |
88,7 |
92,3 |
92,7 |
90,2 |
88,7 |
|
315 |
89,6 |
93,4 |
93,8 |
91,2 |
89,6 |
|
400 |
89,7 |
95,9 |
87,4 |
90,5 |
84,2 |
|
500 |
90,6 |
97,2 |
87,9 |
91,5 |
83,3 |
|
630 |
93,8 |
98,5 |
92,5 |
94,3 |
91,2 |
|
800 |
100,6 |
104,4 |
106,0 |
105,5 |
101,2 |
|
1.000 |
104,7 |
108,3 |
109,9 |
109,4 |
105,2 |
|
1.250 |
106,3 |
109,9 |
111,5 |
111,0 |
106,8 |
|
1.600 |
107,1 |
107,8 |
109,2 |
108,1 |
106,4 |
|
2.000 |
108,8 |
109,6 |
111,0 |
109,9 |
108,0 |
|
2.500 |
109,3 |
110,2 |
111,8 |
110,6 |
108,3 |
|
3.150 |
109,4 |
96,0 |
107,5 |
106,6 |
105,0 |
|
4.000 |
109,7 |
98,4 |
106,8 |
105,2 |
100,9 |
|
5.000 |
110,0 |
98,8 |
107,0 |
105,3 |
100,4 |
|
6.300 |
109,8 |
98,8 |
96,1 |
106,2 |
97,7 |
|
8.000 |
110,0 |
99,1 |
96,4 |
106,2 |
98,0 |
|
10.000 |
110,5 |
99,7 |
97,0 |
106,6 |
98,6 |
Bodemfactor
Voor de Gs-waarde in de in deze bijlage opgenomen rekenmethode geldt een modelleervoorschrift. De gebruiker van de rekensoftware moet de bodemfactor kiezen die bij de afleiding van de Nederlandse bovenbouwcorrrectie gebruikt is. Deze is in tabel 2.3.g opgenomen.
|
Bovenbouw |
Gs |
Bovenbouw |
Gs |
|
|---|---|---|---|---|
|
bb=1 |
1 |
bb=10 |
1 |
|
|
bb=2 |
1 |
bb=11 |
1 |
|
|
bb=3 |
1 |
bb=12 |
1 |
|
|
bb=4 |
0 |
Tramspoor: |
||
|
bb=5 |
1 |
in ballast |
1 |
|
|
bb=6 |
0 |
grasbaan |
1 |
|
|
bb=7 |
1 |
in asfalt |
0 |
|
|
bb=8 |
0 |
tramplaten |
0 |
|
|
bb=9 |
0 |
in klinkers |
0 |
|
Ruwheid
In tabel 2.3.h zijn de railruwheid Lr,TR, de voegruwheid voor stootgeluid LR,IMPACT en de relevante contactfilters A3 opgenomen.
|
Golflengte [mm] |
Lr,TR,i |
LR,IMPACT,i ‘NL’ |
A3 ‘100 kN | 920 mm’ |
A3 ‘50 kN | 680 mm’ |
|---|---|---|---|---|
|
2.000 |
35,0 |
22,0 |
0,0 |
0,0 |
|
1.600 |
31,0 |
22,0 |
0,0 |
0,0 |
|
1.250 |
28,0 |
22,0 |
0,0 |
0,0 |
|
1.000 |
25,0 |
22,0 |
0,0 |
0,0 |
|
800 |
23,0 |
22,0 |
0,0 |
0,0 |
|
630 |
20,0 |
20,0 |
0,0 |
0,0 |
|
500 |
17,0 |
16,0 |
0,0 |
0,0 |
|
400 |
13,5 |
15,0 |
0,0 |
0,0 |
|
315 |
10,5 |
14,0 |
0,0 |
0,0 |
|
250 |
9,0 |
15,0 |
0,0 |
0,0 |
|
200 |
6,5 |
14,0 |
0,0 |
0,0 |
|
160 |
5,5 |
12,0 |
–0,1 |
0,0 |
|
125 |
5,0 |
11,0 |
–0,2 |
0,0 |
|
100 |
3,5 |
10,0 |
–0,3 |
–0,1 |
|
80 |
2,0 |
9,0 |
–0,6 |
–0,2 |
|
63 |
0,1 |
8,0 |
–1,0 |
–0,3 |
|
50 |
–0,2 |
6,0 |
–1,8 |
–0,7 |
|
40 |
–0,3 |
3,0 |
–3,2 |
–1,2 |
|
31,5 |
–0,8 |
2,0 |
–5,4 |
–2,0 |
|
25 |
–3,0 |
–3,0 |
–8,7 |
–4,1 |
|
20 |
–5,0 |
–8,0 |
–12,2 |
–6,0 |
|
16 |
–7,0 |
–13,0 |
–16,7 |
–9,2 |
|
12,5 |
–8,0 |
–17,0 |
–17,7 |
–13,8 |
|
10 |
–9,0 |
–19,0 |
–17,8 |
–17,2 |
|
8 |
–10,0 |
–22,0 |
–20,7 |
–17,7 |
|
6,3 |
–12,0 |
–25,0 |
–22,1 |
–18,6 |
|
5 |
–13,0 |
–26,0 |
–22,8 |
–21,5 |
|
4 |
–14,0 |
–32,0 |
–24,0 |
–22,3 |
|
3,15 |
–15,0 |
–35,0 |
–24,5 |
–23,1 |
|
2,5 |
–16,0 |
–40,0 |
–24,7 |
–24,4 |
|
2 |
–17,0 |
–43,0 |
–27,0 |
–24,5 |
|
1,6 |
–18,0 |
–45,0 |
–27,8 |
–25,0 |
|
1,25 |
–19,0 |
–47,0 |
–28,6 |
–28,0 |
|
1 |
–19,0 |
–49,0 |
–29,4 |
–28,8 |
|
0,8 |
–19,0 |
–50,0 |
–30,2 |
–29,6 |
Bruggeluid
De brugoverdrachtsfunctie LH,bridge en spooroverdrachtsfunctie LH,TR die voor een stalen spoorbrug worden gehanteerd, hangen enkel af van de voor die spoorbrug vastgestelde toeslagwaarden in de 500 Hz en 1.000 Hz octaafband. De voor spoorvoertuigcategorie 8 vastgestelde waarden in die octaafbanden worden daartoe rekenkundig gemiddeld en afgerond op een geheel getal.
|
Afgerond gemiddelde van de toeslag in de 500 Hz en 1.000 Hz octaafband |
Spooroverdrachtsfunctie van Tabel 2.3.d |
Brugoverdrachtsfunctie volgens spectrumnummer sn van Tabel 2.3.i2 |
|---|---|---|
|
0 dB of minder |
bb=1 |
sn=1 |
|
1 dB |
bb=1 |
sn=2 |
|
2 dB |
bb=1 |
sn=3 |
|
3 dB |
bb=1 |
sn=4 |
|
4 dB |
bb=1 |
sn=5 |
|
5 dB |
bb=1 |
sn=6 |
|
6 dB |
bb=8 |
sn=4 |
|
7 dB |
bb=8 |
sn=5 |
|
8 dB |
bb=8 |
sn=6 |
|
9 dB |
bb=6 |
sn=5 |
|
10 dB |
bb=6 |
sn=7 |
|
11 dB |
bb=6 |
sn=8 |
|
12 dB of meer |
bb=6 |
sn=9 |
|
Frequentie [Hz] |
sn=1 |
sn=2 |
sn=3 |
sn=4 |
sn=5 |
sn=6 |
sn=7 |
sn=8 |
sn=9 |
|---|---|---|---|---|---|---|---|---|---|
|
50 |
76,2 |
78,2 |
80,2 |
82,2 |
83,2 |
84,2 |
85,2 |
87,2 |
89,2 |
|
63 |
78,1 |
80,1 |
82,1 |
84,1 |
85,1 |
86,1 |
87,1 |
89,1 |
91,1 |
|
80 |
82,0 |
84,0 |
86,0 |
88,0 |
89,0 |
90,0 |
91,0 |
93,0 |
95,0 |
|
100 |
85,0 |
87,0 |
89,0 |
91,0 |
92,0 |
93,0 |
94,0 |
96,0 |
98,0 |
|
125 |
85,4 |
87,4 |
89,4 |
91,4 |
92,4 |
93,4 |
94,4 |
96,4 |
98,4 |
|
160 |
87,0 |
89,0 |
91,0 |
93,0 |
94,0 |
95,0 |
96,0 |
98,0 |
100,0 |
|
200 |
83,5 |
85,5 |
87,5 |
89,5 |
90,5 |
91,5 |
92,5 |
94,5 |
96,5 |
|
250 |
87,7 |
89,7 |
91,7 |
93,7 |
94,7 |
95,7 |
96,7 |
98,7 |
100,7 |
|
315 |
88,4 |
90,4 |
92,4 |
94,4 |
95,4 |
96,4 |
97,4 |
99,4 |
101,4 |
|
400 |
90,4 |
92,4 |
94,4 |
96,4 |
97,4 |
98,4 |
99,4 |
101,4 |
103,4 |
|
500 |
91,7 |
93,7 |
95,7 |
97,7 |
98,7 |
99,7 |
100,7 |
102,7 |
104,7 |
|
630 |
93,5 |
95,5 |
97,5 |
99,5 |
100,5 |
101,5 |
102,5 |
104,5 |
106,5 |
|
800 |
98,1 |
100,1 |
102,1 |
104,1 |
105,1 |
106,1 |
107,1 |
109,1 |
111,1 |
|
1.000 |
100,8 |
102,8 |
104,8 |
106,8 |
107,8 |
108,8 |
109,8 |
111,8 |
113,8 |
|
1.250 |
103,0 |
105,0 |
107,0 |
109,0 |
110,0 |
111,0 |
112,0 |
114,0 |
116,0 |
|
1.600 |
98,2 |
100,2 |
102,2 |
104,2 |
105,2 |
106,2 |
107,2 |
109,2 |
111,2 |
|
2.000 |
97,8 |
99,8 |
101,8 |
103,8 |
104,8 |
105,8 |
106,8 |
108,8 |
110,8 |
|
2.500 |
98,3 |
100,3 |
102,3 |
104,3 |
105,3 |
106,3 |
107,3 |
109,3 |
111,3 |
|
3.150 |
90,3 |
92,3 |
94,3 |
96,3 |
97,3 |
98,3 |
99,3 |
101,3 |
103,3 |
|
4.000 |
82,4 |
84,4 |
86,4 |
88,4 |
89,4 |
90,4 |
91,4 |
93,4 |
95,4 |
|
5.000 |
77,9 |
79,9 |
81,9 |
83,9 |
84,9 |
85,9 |
86,9 |
88,9 |
90,9 |
|
6.300 |
70,7 |
72,7 |
74,7 |
76,7 |
77,7 |
78,7 |
79,7 |
81,7 |
83,7 |
|
8.000 |
66,1 |
68,1 |
70,1 |
72,1 |
73,1 |
74,1 |
75,1 |
77,1 |
79,1 |
|
10.000 |
61,8 |
63,8 |
65,8 |
67,8 |
68,8 |
69,8 |
70,8 |
72,8 |
74,8 |
Voor betonnen bruggen wordt de brugoverdrachtsfunctie van sn=1 gebruikt in combinatie met de spooroverdrachtsfunctie horende bij bovenbouw die op de brug aanwezig is.
Voertuigparameters
|
Voertuigtype |
Voertuiglengte |
Na/ voertuig |
LH,VEH |
LW,0,idling |
A3 |
Lr,VEH |
|---|---|---|---|---|---|---|
|
Cat 1 |
26 |
4 |
‘920 mm’ |
‘cat1 | A’ |
‘100 kN | 920 mm’ |
De wielruwheid is voor elke categorie apart bepaald. De parameterwaarden staan in tabel 2.3.m |
|
Cat 2 |
26,6 |
4 |
‘920 mm’ |
nvt |
‘100 kN | 920 mm’ |
|
|
Cat 3 |
26,1 |
4 |
‘920 mm’ |
‘cat3 | A’ |
‘100 kN | 920 mm’ |
|
|
Cat 4 |
15 |
4 |
‘920 mm’ |
nvt |
‘100 kN | 920 mm’ |
|
|
Cat 5 |
15 |
4 |
‘920 mm’ |
‘cat5 | AB’ |
‘100 kN | 920 mm’ |
|
|
Cat 6 |
26,2 |
4 |
‘920 mm’ |
‘cat6 | AB’ |
‘100 kN | 920 mm’ |
|
|
Cat 7 |
30 |
6 |
‘680 mm’ |
nvt |
‘50 kN | 680 mm’ |
|
|
Cat 8 |
27 |
4 |
‘920 mm’ |
‘cat8 | A’ |
‘100 kN | 920 mm’ |
|
|
Cat 91 |
199 |
25 |
‘920 mm’ |
‘cat9 | AB’ |
‘100 kN | 920 mm’ |
|
|
Cat 10 |
15 |
3 |
‘A32’ |
‘cat10 | A’ |
‘50 kN | 680 mm’ |
|
|
Cat 11 |
15 |
4 |
‘920 mm’ |
nvt |
‘100 kN | 920 mm’ |
|
|
Cat 12 |
19,2 |
2,6 |
‘840 mm’ |
‘cat12 | A’ |
‘100 kN | 920 mm’ |
|
|
Trams |
29 |
6 |
‘680 mm’ |
nvt |
‘50 kN | 680 mm’ |
|
Frequentie[Hz] |
‘920 mm’ |
‘840 mm’ |
‘680 mm’ |
‘A32’ |
|---|---|---|---|---|
|
50 |
75,4 |
75,4 |
75,4 |
62,7 |
|
63 |
77,3 |
77,3 |
77,3 |
67,6 |
|
80 |
81,1 |
81,1 |
81,1 |
70,6 |
|
100 |
84,1 |
84,1 |
84,1 |
80,4 |
|
125 |
83,3 |
82,8 |
82,8 |
84,4 |
|
160 |
84,3 |
83,3 |
83,3 |
89,0 |
|
200 |
86,0 |
84,1 |
83,9 |
87,9 |
|
250 |
90,1 |
86,9 |
86,3 |
87,7 |
|
315 |
89,8 |
87,9 |
88,0 |
81,4 |
|
400 |
89,0 |
89,9 |
92,2 |
77,6 |
|
500 |
88,8 |
90,9 |
93,9 |
85,6 |
|
630 |
90,4 |
91,5 |
92,5 |
89,1 |
|
800 |
92,4 |
91,5 |
90,9 |
90,9 |
|
1.000 |
94,9 |
93,0 |
90,4 |
96,1 |
|
1.250 |
100,4 |
98,7 |
93,2 |
98,0 |
|
1.600 |
104,6 |
101,6 |
93,5 |
108,0 |
|
2.000 |
109,6 |
107,6 |
99,6 |
112,0 |
|
2.500 |
114,9 |
111,9 |
104,9 |
113,0 |
|
3.150 |
115,0 |
114,5 |
108,0 |
105,0 |
|
4.000 |
115,0 |
114,5 |
111,0 |
107,0 |
|
5.000 |
115,5 |
115,0 |
111,5 |
103,0 |
|
6.300 |
115,6 |
115,1 |
111,6 |
99,9 |
|
8.000 |
116,0 |
115,5 |
112,0 |
100,3 |
|
10.000 |
116,7 |
116,2 |
112,7 |
101,0 |
|
Frequentie [Hz] |
‘cat1 | A’ |
‘cat3 | A’ |
‘cat5 | AB’ |
‘cat6 | AB’ |
‘cat8 | A’ |
‘cat9 | AB’ |
‘cat10 | A’ |
‘cat12 | A’ |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
50 |
0,0 |
0 |
0,0 |
0 |
109,0 |
109,0 |
0,0 |
0,0 |
99,6 |
0 |
98,0 |
98,0 |
0,0 |
0 |
0 |
0 |
|
63 |
0,0 |
0 |
0,0 |
0 |
109,0 |
109,0 |
0,0 |
0,0 |
99,6 |
0 |
98,0 |
98,0 |
0,0 |
0 |
0 |
0 |
|
80 |
0,0 |
0 |
0,0 |
0 |
109,0 |
109,0 |
0,0 |
0,0 |
99,6 |
0 |
98,0 |
98,0 |
0,0 |
0 |
0 |
0 |
|
100 |
0,0 |
0 |
97,0 |
0 |
95,0 |
95,0 |
93,1 |
93,1 |
86,6 |
0 |
98,0 |
98,0 |
95,7 |
0 |
100,6 |
0 |
|
125 |
0,0 |
0 |
97,0 |
0 |
95,0 |
95,0 |
93,1 |
93,1 |
86,6 |
0 |
98,0 |
98,0 |
95,7 |
0 |
100,6 |
0 |
|
160 |
0,0 |
0 |
97,0 |
0 |
95,0 |
95,0 |
93,1 |
93,1 |
86,6 |
0 |
98,0 |
98,0 |
95,7 |
0 |
100,6 |
0 |
|
200 |
98,1 |
0 |
107,0 |
0 |
103,0 |
103,0 |
103,1 |
103,1 |
95,6 |
0 |
101,0 |
98,7 |
0,0 |
0 |
86,6 |
0 |
|
250 |
98,1 |
0 |
107,0 |
0 |
103,0 |
103,0 |
103,1 |
103,1 |
95,6 |
0 |
101,0 |
98,7 |
0,0 |
0 |
86,6 |
0 |
|
315 |
98,1 |
0 |
107,0 |
0 |
103,0 |
103,0 |
103,1 |
103,1 |
95,6 |
0 |
101,0 |
98,7 |
0,0 |
0 |
86,6 |
0 |
|
400 |
0,0 |
0 |
0,0 |
0 |
103,0 |
103,0 |
0,0 |
0,0 |
101,6 |
0 |
106,0 |
103,7 |
0,0 |
0 |
98,6 |
0 |
|
500 |
0,0 |
0 |
0,0 |
0 |
103,0 |
103,0 |
0,0 |
0,0 |
101,6 |
0 |
106,0 |
103,7 |
0,0 |
0 |
98,6 |
0 |
|
630 |
0,0 |
0 |
0,0 |
0 |
103,0 |
103,0 |
0,0 |
0,0 |
101,6 |
0 |
106,0 |
103,7 |
0,0 |
0 |
98,6 |
0 |
|
800 |
0,0 |
0 |
0,0 |
0 |
94,0 |
94,0 |
0,0 |
0,0 |
96,6 |
0 |
104,0 |
101,7 |
0,0 |
0 |
0 |
0 |
|
1.000 |
0,0 |
0 |
0,0 |
0 |
94,0 |
94,0 |
0,0 |
0,0 |
96,6 |
0 |
104,0 |
101,7 |
0,0 |
0 |
0 |
0 |
|
1.250 |
0,0 |
0 |
0,0 |
0 |
94,0 |
94,0 |
0,0 |
0,0 |
96,6 |
0 |
104,0 |
101,7 |
0,0 |
0 |
0 |
0 |
|
1.600 |
0,0 |
0 |
0,0 |
0 |
96,0 |
96,0 |
0,0 |
0,0 |
0,0 |
0 |
94,0 |
91,7 |
0,0 |
0 |
0 |
0 |
|
2.000 |
0,0 |
0 |
0,0 |
0 |
96,0 |
96,0 |
0,0 |
0,0 |
0,0 |
0 |
94,0 |
91,7 |
0,0 |
0 |
0 |
0 |
|
2.500 |
0,0 |
0 |
0,0 |
0 |
96,0 |
96,0 |
0,0 |
0,0 |
0,0 |
0 |
94,0 |
91,7 |
0,0 |
0 |
0 |
0 |
|
3.150 |
0,0 |
0 |
0,0 |
0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0 |
95,0 |
92,7 |
0,0 |
0 |
0 |
0 |
|
4.000 |
0,0 |
0 |
0,0 |
0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0 |
95,0 |
92,7 |
0,0 |
0 |
0 |
0 |
|
5.000 |
0,0 |
0 |
0,0 |
0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0 |
95,0 |
92,7 |
0,0 |
0 |
0 |
0 |
|
6.300 |
0,0 |
0 |
0,0 |
0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0 |
92,0 |
89,7 |
0,0 |
0 |
0 |
0 |
|
8.000 |
0,0 |
0 |
0,0 |
0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0 |
92,0 |
89,7 |
0,0 |
0 |
0 |
0 |
|
10.000 |
0,0 |
0 |
0,0 |
0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0 |
92,0 |
89,7 |
0,0 |
0 |
0 |
0 |
|
Golflengte [mm] |
Cat 1 |
Cat 2 |
Cat 3 |
Cat 4 |
Cat 5 |
Cat 6 |
Cat 7 |
Cat 8 |
Cat 9 |
Cat 10 |
Cat 11 |
Cat 12 |
Trams |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
2.000 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
29,9 |
24,8 |
25,1 |
24,8 |
24,8 |
24,0 |
12,3 |
|
1.600 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
29,9 |
24,8 |
25,1 |
24,8 |
24,8 |
24,0 |
12,3 |
|
1.250 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
28,5 |
24,8 |
22,1 |
24,8 |
24,8 |
24,0 |
12,3 |
|
1.000 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
27,6 |
24,8 |
20,0 |
24,8 |
24,8 |
24,0 |
12,3 |
|
800 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
24,8 |
27,2 |
24,8 |
19,0 |
24,8 |
24,8 |
24,0 |
12,3 |
|
630 |
23,3 |
23,3 |
23,3 |
24,7 |
24,7 |
23,3 |
25,4 |
23,3 |
14,0 |
24,0 |
23,3 |
24,0 |
12,3 |
|
500 |
14,7 |
21,7 |
14,7 |
17,0 |
17,0 |
14,7 |
19,7 |
14,7 |
9,0 |
14,0 |
14,7 |
22,0 |
12,3 |
|
400 |
11,0 |
17,6 |
14,0 |
11,0 |
11,0 |
12,4 |
16,9 |
9,7 |
7,0 |
11,0 |
9,7 |
20,0 |
12,3 |
|
315 |
10,0 |
14,6 |
12,0 |
10,0 |
10,0 |
9,4 |
13,2 |
6,7 |
1,4 |
10,0 |
15,9 |
21,0 |
12,3 |
|
250 |
7,0 |
13,7 |
11,0 |
10,0 |
10,0 |
6,7 |
9,1 |
6,7 |
3,1 |
8,0 |
16,3 |
17,0 |
12,3 |
|
200 |
6,0 |
14,3 |
11,0 |
8,0 |
8,0 |
7,4 |
8,4 |
5,4 |
5,4 |
6,0 |
13,0 |
14,0 |
12,9 |
|
160 |
5,2 |
14,6 |
10,1 |
9,1 |
9,1 |
9,7 |
8,9 |
8,3 |
6,6 |
4,0 |
13,1 |
12,0 |
10,9 |
|
125 |
8,3 |
14,7 |
9,3 |
12,2 |
12,2 |
7,1 |
6,1 |
8,6 |
6,4 |
2,0 |
12,2 |
11,0 |
8,0 |
|
100 |
7,4 |
15,0 |
4,9 |
13,3 |
13,3 |
4,9 |
7,0 |
8,4 |
4,6 |
–3,4 |
9,4 |
10,0 |
5,2 |
|
80 |
5,6 |
14,3 |
6,2 |
12,2 |
12,2 |
6,2 |
6,5 |
6,5 |
5,6 |
–4,7 |
8,5 |
9,0 |
1,4 |
|
63 |
6,5 |
13,8 |
4,7 |
10,6 |
10,6 |
4,7 |
3,6 |
7,5 |
6,5 |
–6,4 |
5,3 |
8,0 |
–1,7 |
|
50 |
7,6 |
10,4 |
4,6 |
10,4 |
9,6 |
4,6 |
–0,4 |
4,7 |
0,9 |
–6,9 |
4,7 |
0,0 |
–3,9 |
|
40 |
8,2 |
10,9 |
5,1 |
8,6 |
7,2 |
5,1 |
–0,9 |
4,4 |
1,8 |
–6,5 |
0,9 |
–6,0 |
–6,1 |
|
31,5 |
8,9 |
8,9 |
1,3 |
8,9 |
8,0 |
1,3 |
–0,9 |
1,2 |
3,5 |
–7,2 |
1,3 |
–8,0 |
–7,2 |
|
25 |
10,1 |
10,5 |
3,9 |
9,2 |
9,2 |
3,9 |
0,1 |
2,3 |
3,8 |
–6,2 |
3,1 |
–2,0 |
–6,2 |
|
20 |
11,3 |
12,3 |
4,7 |
8,4 |
8,4 |
4,7 |
0,5 |
4,7 |
3,9 |
–7,3 |
2,2 |
–2,0 |
–7,6 |
|
16 |
12,3 |
12,3 |
7,6 |
12,3 |
12,3 |
7,6 |
0,5 |
5,4 |
4,1 |
–7,6 |
3,3 |
5,0 |
–7,8 |
|
12,5 |
7,6 |
6,6 |
5,5 |
8,4 |
8,4 |
5,5 |
2,1 |
1,2 |
2,3 |
–6,2 |
5,7 |
1,0 |
–6,2 |
|
10 |
3,5 |
5,3 |
4,7 |
4,4 |
4,4 |
4,7 |
5,6 |
–1,3 |
0,3 |
–4,6 |
3,5 |
–2,0 |
–4,7 |
|
8 |
4,6 |
4,3 |
4,6 |
5,2 |
5,2 |
4,6 |
0,9 |
–1,8 |
–0,2 |
–5,6 |
2,4 |
–2,0 |
–5,7 |
|
6,3 |
–0,2 |
–0,2 |
0,8 |
2,7 |
2,7 |
0,8 |
–0,1 |
–2,9 |
0,3 |
–7,6 |
1,9 |
–1,0 |
–7,8 |
|
5 |
–1,5 |
–1,5 |
0,7 |
0,4 |
0,4 |
0,7 |
2,0 |
–5,3 |
–1,5 |
–8,1 |
–1,3 |
–2,0 |
–8,3 |
|
4 |
–5,6 |
–5,6 |
–0,2 |
–4,1 |
–0,8 |
–0,2 |
–1,4 |
–7,1 |
–4,1 |
–8,0 |
–4,1 |
–6,0 |
–8,2 |
|
3,15 |
–7,2 |
–8,4 |
–2,8 |
–5,7 |
–2,4 |
–2,8 |
–2,6 |
–9,3 |
–6,0 |
–8,8 |
–5,7 |
–5,0 |
–8,8 |
|
2,5 |
–12,1 |
–11,6 |
–7,9 |
–9,1 |
–6,0 |
–7,9 |
–2,3 |
–11,7 |
–6,8 |
–9,0 |
–9,1 |
–5,0 |
–8,9 |
|
2 |
–11,4 |
–9,8 |
–7,5 |
–9,1 |
–5,6 |
–7,5 |
–4,2 |
–11,0 |
–5,3 |
–11,1 |
–9,1 |
–7,0 |
–11,0 |
|
1,6 |
–12,5 |
–9,8 |
–7,6 |
–10,3 |
–6,7 |
–7,6 |
–5,8 |
–12,5 |
–5,4 |
–12,6 |
–10,3 |
–10,0 |
–12,6 |
|
1,25 |
–13,5 |
–10,5 |
–8,1 |
–11,6 |
–8,0 |
–8,1 |
–4,1 |
–13,9 |
–5,9 |
–11,2 |
–11,6 |
–13,0 |
–11,4 |
|
1 |
–13,8 |
–10,8 |
–8,3 |
–12,4 |
–9,8 |
–8,3 |
–4,3 |
–14,7 |
–6,1 |
–11,5 |
–12,4 |
–15,0 |
–11,6 |
|
0,8 |
–13,9 |
–10,9 |
–8,4 |
–12,5 |
–11,3 |
–8,4 |
–4,5 |
–15,2 |
–6,2 |
–11,7 |
–12,5 |
–15,0 |
–11,9 |
|
Frequentie [Hz] |
‘Cat9 aero’ LW,0,1 | LW,0,2 |
Frequentie [Hz] |
‘Cat9 aero’ LW,0,1 | LW,0,2 |
|||
|---|---|---|---|---|---|---|
|
alpha |
50 |
50 |
||||
|
50 |
135,0 |
129,0 |
800 |
125,5 |
119,5 |
|
|
63 |
135,0 |
129,0 |
1.000 |
125,5 |
119,5 |
|
|
80 |
135,0 |
129,0 |
1.250 |
125,5 |
119,5 |
|
|
100 |
128,0 |
122,0 |
1.600 |
128,0 |
125,0 |
|
|
125 |
128,0 |
122,0 |
2.000 |
128,0 |
125,0 |
|
|
160 |
128,0 |
122,0 |
2.500 |
128,0 |
125,0 |
|
|
200 |
127,0 |
121,0 |
3.150 |
123,0 |
117,0 |
|
|
250 |
127,0 |
121,0 |
4.000 |
123,0 |
117,0 |
|
|
315 |
127,0 |
121,0 |
5.000 |
123,0 |
117,0 |
|
|
400 |
125,5 |
119,5 |
6.300 |
119,0 |
113,0 |
|
|
500 |
125,5 |
119,5 |
8.000 |
119,0 |
113,0 |
|
|
630 |
125,5 |
119,5 |
10.000 |
119,0 |
113,0 |
|
Classificatie van brontypen (punt, lijn, diffuus)
De afmetingen van de industriebronnen zijn zeer uiteenlopend. Ze kunnen zowel grote industriële fabrieken als kleine geconcentreerde bronnen zijn, zoals klein gereedschap of fabrieksmachines. Daarom moet voor de specifieke ter beoordeling voorliggende bron een relevante modelleringstechniek worden gebruikt. Afhankelijk van de omvang en de wijze waarop verschillende individuele bronnen zich over een gebied uitstrekken, waarbij elke bron tot hetzelfde industrieterrein behoort, kunnen deze als puntbronnen, bronlijnen of diffuse bronnen worden gemodelleerd. In de praktijk worden de berekeningen van het geluidseffect altijd op puntbronnen gebaseerd, maar verschillende puntbronnen kunnen worden gebruikt om een bijzonder complexe bron weer te geven, die zich hoofdzakelijk over een lijn of gebied uitstrekt.
Aantal en plaats van equivalente geluidsbronnen
De werkelijke geluidsbronnen worden gemodelleerd door middel van equivalente geluidsbronnen die door een of meer puntbronnen worden weergegeven zodat het totale geluidsvermogen van de werkelijke bron overeenkomt met de som van de individuele geluidsvermogens die toe te schrijven zijn aan de verschillende puntbronnen.
De algemene regels die bij de bepaling van het aantal te gebruiken puntbronnen worden toegepast, zijn:
• lijn- of oppervlaktebronnen waarvan de grootste diameter minder dan de helft van de afstand tussen de bron en het waarneempunt is, kunnen als individuele puntbronnen worden gemodelleerd;
• bronnen waarvan de grootste afmeting meer dan de helft van de afstand tussen de bron en het waarneempunt is, moeten als een reeks incoherente puntbronnen in een lijn of als een reeks incoherente puntbronnen over een gebied worden gemodelleerd, zodanig dat voor elk van deze bronnen aan de voorwaarde van de halve afstand wordt voldaan. De verdeling over een gebied kan een verticale verdeling van puntbronnen omvatten;
• voor bronnen waarvan de grootste hoogteafmetingen meer dan 2 m bedragen of die vlakbij de grond zijn, moet bijzondere aandacht aan de hoogte van de bron worden besteed. Verdubbeling van het aantal bronnen, door ze alleen in de z-component te herverdelen, leidt niet noodzakelijkerwijs tot aanzienlijk betere resultaten voor deze bron;
• voor elke bron geldt dat een verdubbeling van het aantal bronnen over het brongebied (in alle dimensies) niet noodzakelijkerwijs tot aanzienlijk betere resultaten leidt.
Een vaste positie van de equivalente geluidsbronnen is niet mogelijk, gezien het grote aantal configuraties dat een industrieterrein kan hebben. Goede praktijken zijn normaliter van toepassing.
Geluidsvermogensemissie
Algemeen
De volgende informatie omvat de volledige reeks invoergegevens voor berekeningen van geluidsvoortplanting met de methoden die voor geluidskartering worden gebruikt:
• uitgestraald geluidsvermogensspectrum in octaafbanden,
• bedrijfstijden (overdag, 's avonds, 's nachts, op basis van jaarlijks gemiddelde),
• locatie (coördinaten x, y) en hoogte (z) van de geluidsbron,
• soort bron (punt, lijn, diffuus),
• afmetingen en oriëntatie,
• bedrijfscondities van de bron,
• richteffect van de bron.
Het geluidsvermogen van de puntbron en diffuse bron moet worden gedefinieerd als:
• voor een puntbron, geluidsvermogen Lw en richteffect als een functie van de drie orthogonale coördinaten (x,y,z),
• voor een diffuse bron, geluidsvermogen per vierkante meter Lw/m2, en geen richteffect (kan horizontaal of verticaal zijn).
Het geluidsvermogen van twee typen bronlijnen moet worden gedefinieerd als:
• bronlijnen die transportbanden, pijpleidingen enz., weergeven, geluidsvermogen per meter lengte Lw’ en richteffect als een functie van de twee orthogonale coördinaten op de as van de bronlijn,
• bronlijnen die rijdende voertuigen weergeven, worden berekend volgens formule 2.2.1
De invoer van de bedrijfsuren is essentieel voor de berekening van geluidsniveaus. De bedrijfsuren worden voor de dag-, avond- en nachtperiode gegeven en, als de voortplanting afwijkende meteorologische categorieën gebruikt die tijdens elke dag-, nacht- en avondperiode zijn gedefinieerd, wordt een verfijnde verdeling van de bedrijfsuren gegeven in deelperioden die congrueren met de verdeling van meteorologische categorieën. Deze informatie berust op een jaarlijks gemiddelde.
De correctie voor de bedrijfsuren, die aan het brongeluidsvermogen wordt toegevoegd om het gecorrigeerde geluidsvermogen te bepalen dat voor de berekeningen over elke tijdsperiode CW in dB wordt gebruikt, wordt als volgt berekend:
|
|
(2.4.1) |
waarbij:
T de actieve brontijd per periode is op basis van een jaarlijks gemiddelde situatie, in uren;
Tref de referentieperiode in uren is (bv. dag is 12 uur, avond is 4 uur, nacht is 8 uur).
Voor de dominantere bronnen wordt de correctie van de jaarlijkse gemiddelde bedrijfsuren binnen minstens 0,5 dB tolerantie geschat om een aanvaardbare nauwkeurigheid (die gelijk is aan een onzekerheid van minder dan 10% in de definitie van de actieve brontijd) te verkrijgen.
Richteffect van de bron
Het richteffect van de bron is nauw verbonden met de positie van de equivalente geluidsbron naast of vlakbij oppervlakken. Omdat de voortplantingsmethode met de reflectie van het nabijgelegen oppervlak en de geluidsabsorptie ervan rekening houdt, is het noodzakelijk om de locatie van de nabijgelegen oppervlakken zorgvuldig in aanmerking te nemen. In het algemeen worden de volgende twee gevallen altijd onderscheiden:
• brongeluidsvermogen en richteffect worden ten opzichte van een bepaalde werkelijke bron bepaald en gegeven wanneer die zich in vrij veld bevindt (exclusief het terreineffect). Dit is in overeenstemming met de definities met betrekking tot de voortplanting, indien aangenomen wordt dat er zich geen nabijgelegen oppervlak op minder dan 0,01 m van de bron bevindt en dat oppervlakken op een afstand van 0,01 m of meer in de berekening van de voortplanting worden opgenomen;
• brongeluidsvermogen en richteffect worden ten opzichte van een bepaalde werkelijke bron bepaald en gegeven wanneer die in een specifieke locatie is geplaatst, en daarom zijn brongeluidsvermogen en richteffect in feite ‘equivalent’ omdat ze de modellering van het effect van de nabijgelegen oppervlakken bevatten. Dit wordt bepaald in het ‘half-vrije veld’ volgens de definities met betrekking tot de voortplanting. In dit geval worden de gemodelleerde nabijgelegen oppervlakken van de berekening van de voortplanting uitgesloten.
Het richteffect wordt in de berekening uitgedrukt als een
factor ∆LW,dir,xyz(x,y,z) die aan het
geluidsvermogen wordt toegevoegd om het juiste richtingsafhankelijke
geluidsvermogen van een referentiegeluidsbron te verkrijgen, zoals gezien door
de geluidsvoortplanting in de gegeven richting. De factor kan worden gegeven
als een functie van de richtingsvector gedefinieerd door (x,y,z) met
![]() Dit richteffect kan ook worden uitgedrukt door
middel van andere coördinatensystemen zoals hoekige coördinatenstelsels.
Dit richteffect kan ook worden uitgedrukt door
middel van andere coördinatensystemen zoals hoekige coördinatenstelsels.
Dit document omschrijft een methode voor de berekening van de geluidsdemping tijdens de voortplanting ervan buitenshuis. Met de bekende kenmerken van de bron voorspelt deze methode het equivalente constante geluidsniveau op een waarneempunt dat overeenstemt met twee bepaalde soorten van atmosferische omstandigheden:
• voortplantingscondities met neerwaartse breking (positieve verticale gradiënt van effectieve geluidssnelheid) van de bron naar het waarneempunt,
• homogene atmosferische omstandigheden (geen verticale gradiënt van effectieve geluidssnelheid) over het gehele voortplantingsgebied.
De in dit document beschreven berekeningsmethode is van toepassing voor weg-, spoor- en industriebronnen. Deze methode is daarom met name van toepassing op de infrastructuur van wegen en spoorlijnen. Luchtvervoer wordt alleen in het toepassingsgebied van de methode opgenomen voor het lawaai dat tijdens grondoperaties wordt voortgebracht, waarbij de start en landing worden uitgesloten.
Industriële infrastructuren die impulsieve of sterk tonale geluiden voortbrengen zoals beschreven in ISO 1996-2: 2007, vallen niet onder het toepassingsgebied van deze methode.
De berekeningsmethode levert geen resultaten voor voortplantingscondities met opwaartse breking (negatieve verticale gradiënt van de effectieve geluidssnelheid), maar deze condities worden bij de berekening van Lden door homogene condities benaderd.
Voor de berekening van de demping door atmosferische absorptie in het geval van vervoersinfrastructuur, worden de temperatuur en vochtigheid volgens ISO 9613-1:1996 berekend.
De methode levert resultaten per octaafband van 63 Hz tot 8 000 Hz. De berekeningen worden voor elk van de middenfrequenties verricht.
Objecten die meer dan 15° aflopen in verhouding tot de verticaal worden niet als reflecterende objecten beschouwd, maar worden in aanmerking genomen bij alle andere aspecten van de voortplanting, zoals grondeffecten en diffractie.
Een enkel scherm wordt als een enkele diffractieberekening berekend, twee of meer schermen in een enkel pad worden als een volgende set van enkele diffracties behandeld door toepassing van de procedure die nader wordt omschreven.
Alle afstanden, hoogten, afmetingen in dit document worden in meter (m) uitgedrukt. De notatie MN staat voor de afstand in 3 dimensies (3D) tussen de punten M en N, gemeten volgens een rechte lijn die deze punten verbindt.
Het is gebruikelijk dat werkelijke hoogten verticaal worden gemeten in een richting loodrecht op het horizontale vlak. Hoogten van punten boven de plaatselijke grond worden aangeduid met h, absolute hoogten van punten en de absolute hoogte van de grond worden aangeduid met de letter H.
Om het werkelijke reliëf van de grond langs een voortplantingspad in aanmerking te nemen, is het begrip ‘equivalente hoogte’ ingevoerd, aangeduid met de letter z. Dit vervangt de werkelijke hoogten in de vergelijkingen van het grondeffect.
De geluidsniveaus, aangeduid met de hoofdletter L, worden uitgedrukt in decibel (dB) per frequentieband wanneer index A wordt weggelaten. De geluidsniveaus in decibel dB(A) krijgen de index A.
De som van de geluidsniveaus als gevolg van wederzijds
incoherente bronnen wordt aangeduid met het teken
![]() in overeenstemming met de volgende definitie:
in overeenstemming met de volgende definitie:
|
|
(2.5.1) |
Segmentatie van de bron
Werkelijke bronnen worden beschreven door een reeks puntbronnen of, bij spoorverkeer en wegverkeer, door incoherente bronlijnen. De voortplantingsmethode gaat ervan uit dat lijn- of diffuse bronnen voorafgaand zijn gesplitst om door een aantal equivalente puntbronnen te worden weergegeven. Dit kan bij voorbewerking van de brongegevens zijn opgetreden of in de pathfinder-component van de berekeningssoftware zijn ontstaan. De wijze waarop dit is gebeurd, valt buiten het toepassingsgebied van de onderhavige methode.
Voortplantingspaden
De methode werkt op een geometrisch model dat bestaat uit een reeks verbonden grond- en obstakeloppervlakken. Een verticaal voortplantingspad wordt op een of meerdere verticale vlakken ten opzichte van het horizontale vlak ingezet. Voor trajecten die reflecties op verticale vlakken omvatten die niet orthogonaal op het incidentvlak zijn, wordt daarna een ander verticaal vlak in aanmerking genomen, waaronder het gereflecteerde deel van het voortplantingspad. In deze gevallen, waar meerdere verticale vlakken worden gebruikt om het gehele traject van de bron naar het waarneempunt te beschrijven, worden de verticale vlakken vervolgens afgevlakt, net als een uitvouwend Chinees kamerscherm.
Aanmerkelijke hoogten boven de grond
De equivalente hoogten worden verkregen van het gemiddelde grondvlak tussen de bron en het waarneempunt. Dit vervangt de werkelijke grond met een fictief vlak dat het gemiddelde profiel van de grond weergeeft.
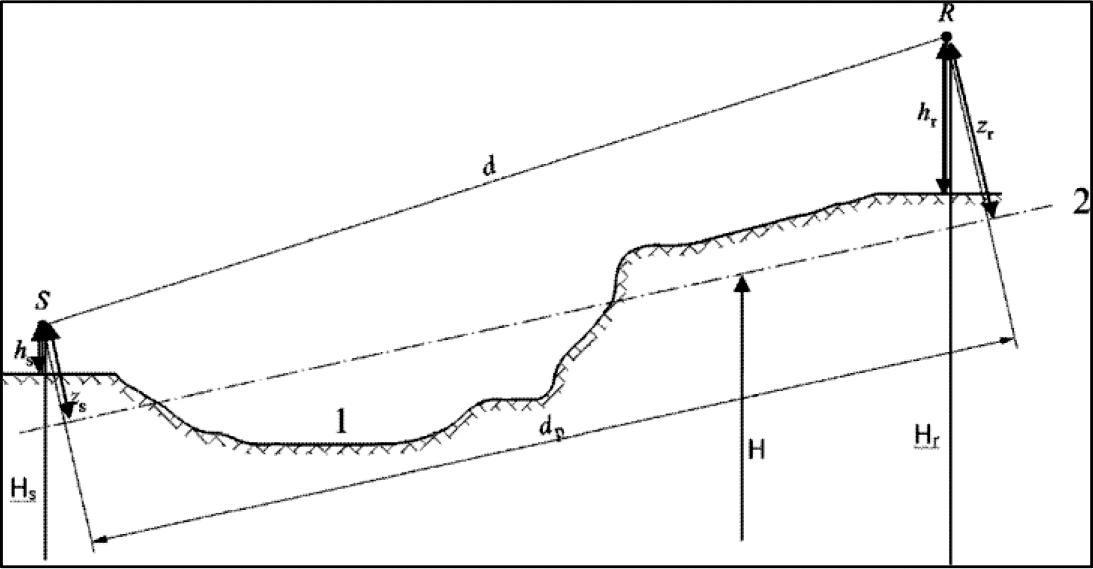
Figuur 2.5.a, Equivalente hoogten in verhouding tot de grond
1: Werkelijk reliëf
2: Gemiddeld vlak
De equivalente hoogte van een punt is zijn orthogonale hoogte in verhouding tot het gemiddelde grondvlak. De equivalente bronhoogte zS en de equivalente hoogte van het waarneempunt z0 kan daarom worden gedefinieerd. De afstand tussen de bron en het waarneempunt geprojecteerd over het gemiddelde grondvlak wordt aangeduid met dp.
Als de equivalente hoogte van een punt negatief wordt, dat wil zeggen als het punt zich onder het gemiddelde grondvlak bevindt, wordt een hoogte van nul aangehouden en dan is het equivalente punt identiek aan zijn eventuele spiegelpunt.
Berekening van het gemiddelde grondvlak
In het vlak van het pad kan de topografie (waaronder terrein, heuvels, spoortaluds en andere kunstmatige obstakels, gebouwen,...) aan de hand van een geordende verzameling van afzonderlijke punten (xk, Hk); k є {1,...,n} worden beschreven. Deze reeks punten definieert een polylijn of, op gelijke wijze, een reeks rechtlijnige segmenten Hk = akx + bk, x є [xk, x(k+1)]; k є {1,...,n}, waarbij:
|
|
(2.5.2) |
Het gemiddelde vlak wordt weergegeven door de rechte lijn Z = ax + b; x є [x1, xn], die aan de polylijn is aangepast door middel van een benadering van het kleinste kwadraat. De vergelijking van de gemiddelde lijn kan analytisch worden uitgewerkt.
Met behulp van:
|
|
(2.5.3) |
worden de coëfficiënten van de rechte lijn verkregen door:
|
|
(2.5.4) |
waarbij segmenten met xk+1 = xk buiten beschouwing worden gelaten bij de beoordeling van vergelijking 2.5.3.
Reflecties door gevels en andere verticale obstakels
Bijdragen van reflectie worden in aanmerking genomen door de invoering van spiegelbronnen, zoals hieronder beschreven.
Voor een waarneempunt R worden de berekeningen uitgevoerd in overeenstemming met de volgende stappen:
1) op elk voortplantingspad:
• berekening van de demping in gunstige omstandigheden,
• berekening van de demping in homogene omstandigheden,
• berekening van langdurig geluidsniveau voor elk pad.
2) accumulatie van de langdurige geluidsniveaus voor alle paden die invloed hebben op een specifiek waarneempunt, zodat het totale geluidsniveau op het waarneempunt kan worden berekend.
Opgemerkt wordt dat alleen demping ten gevolge van het grondeffect (Aground) en diffractie (Adif) door meteorologische omstandigheden wordt beïnvloed.
Voor een puntbron S van richtingsafhankelijk geluidsvermogen LW,0,dir en voor een specifieke frequentieband wordt het equivalente constante geluidsniveau op het waarneempunt R in de gegeven atmosferische omstandigheden volgens de onderstaande vergelijkingen verkregen.
Geluidsniveau in gunstige omstandigheden (LF) voor een pad (S,R)
|
LF = LW,0,dir – AF |
(2.5.5) |
De term AF geeft de totale demping weer langs het voortplantingspad in gunstige omstandigheden, en wordt als volgt uitgesplitst:
|
AF = Adiv + Aatm+Aboundary,F |
(2.5.6) |
waarbij
Adiv de demping door geometrische divergentie is;
Aatm de demping door atmosferische absorptie is;
Aboundary,F de demping door de grens van het voortplantingsmedium in gunstige omstandigheden is. De volgende termen kunnen erin vervat zijn:
• Aground,F, de demping door de grond in gunstige omstandigheden;
• Adif,F, de demping door diffractie in gunstige omstandigheden.
Voor een bepaald pad en bepaalde frequentieband zijn de volgende twee scenario's mogelijk:
• ofwel Aground,F wordt zonder diffractie (Adif,F = 0 dB) en Aboundary,F = Aground,F berekend;
• ofwel Adif,F wordt berekend. Het grondeffect wordt in aanmerking genomen in de Adif,F vergelijking zelf (Aground,F = 0 dB). Dit levert dus Aboundary,F = Adif,F op.
Geluidsniveau in homogene omstandigheden (LH) voor een pad (S,R)
De procedure is volkomen identiek aan het geval van gunstige omstandigheden in het vorige gedeelte.
|
LH = LW,0,dir – AH |
(2.5.7) |
De term AH geeft de totale demping weer langs het voortplantingspad in homogene omstandigheden, en wordt als volgt uitgesplitst:
|
AH = Adiv + Aatm + Aboundary,H |
(2.5.8) |
waarbij
Adiv de demping door geometrische divergentie is;
Aatm de demping door atmosferische absorptie is;
Aboundary,H de demping door de grens van het voortplantingsmedium in homogene omstandigheden is. De volgende termen kunnen erin vervat zijn:
• Aground,H, de demping door de grond in homogene omstandigheden;
• Adif,H, de demping door diffractie in homogene omstandigheden.
Voor een bepaald pad en bepaalde frequentieband zijn de volgende twee scenario's mogelijk:
• ofwel Aground,H (Adif,H = 0 dB) wordt zonder diffractie en Aboundary,H = Aground,H berekend;
• ofwel Adif,H (Aground,H = 0 dB) wordt berekend. Het grondeffect wordt in de vergelijking Adif,H zelf in aanmerking genomen. Dit levert dus Aboundary,H = Adif,H op.
Statistische benadering in stedelijke gebieden voor een pad (S,R)
In stedelijke gebieden is een statistische benadering van de berekening van de geluidsvoortplanting achter de eerste lijn gebouwen eveneens toegestaan, mits deze methode naar behoren wordt gedocumenteerd, met inbegrip van relevante informatie over de kwaliteit van de methode. Deze methode kan de berekening van Aboundary,H en Aboundary,F vervangen door een benadering van de totale demping voor het rechtstreekse pad en alle reflecties. De berekening wordt op de gemiddelde dichtheid en gemiddelde hoogte van alle gebouwen in het gebied gebaseerd.
Langdurig geluidsniveau voor een pad (S,R)
Het ‘langdurige’ geluidsniveau langs een pad, uitgaande van een bepaalde puntbron, wordt verkregen uit de logaritmische som van de gewogen geluidsenergie in homogene omstandigheden en de geluidsenergie in gunstige omstandigheden.
Deze geluidsniveaus worden gewogen door het gemiddelde optreedfrequentie p van gunstige omstandigheden in de richting van het pad (S,R):
|
|
(2.5.9a) |
NB: De gebeurteniswaarden voor p worden in fracties uitgedrukt. Dus indien de frequentie van optreden 82% is, krijgt de vergelijking (2.5.9a) p = 0,82.
Optreedfrequentie per richting en periode
De gebeurteniswaarden voor p zijn richtingsafhankelijk en periode afhankelijk. De waarden p worden berekend met de volgende formules:
|
|
(2.5.9b) |
De voortplantingsrichting ξ is als volgt gedefinieerd:
|
Hoek(ξ) |
Van |
Naar |
|---|---|---|
|
0 |
Noord |
Zuid |
|
90 |
Oost |
West |
|
180 |
Zuid |
Noord |
|
270 |
West |
Oost |
Langdurig geluidsniveau op punt R voor alle paden
Het totale langdurige geluidsniveau op het waarneempunt voor een frequentieband wordt verkregen aan de hand van de energetische optelling van bijdragen van alle N-paden, met inbegrip van alle typen:
|
|
(2.5.10) |
waarbij:
n de index van de paden tussen S en R is.
Het in aanmerking nemen van reflectie door middel van spiegelbronnen wordt hieronder beschreven. De procentuele frequentie van gunstige omstandigheden bij reflectie van een pad op een verticaal obstakel wordt geacht identiek te zijn aan de frequentie van het rechtstreekse pad.
Als S’ de spiegelbron van S is, wordt het optreedfrequentie p’ van het pad (S’, R) beschouwd als gelijk te zijn aan optreedfrequentie p van het pad (Si, R).
Langdurig geluidsniveau op punt R in decibels A (dBA)
Het totale geluidsniveau in decibels A (dBA) wordt verkregen door de niveaus in elke frequentieband op te tellen:
|
|
(2.5.11) |
Waarbij i de index van de frequentieband is. AWC is de A-gewogen correctie als volgt:
|
Frequentie [Hz] |
63 |
125 |
250 |
500 |
1.000 |
2.000 |
4.000 |
8.000 |
|
AWCf,i [dB] |
–26,2 |
–16,1 |
–8,6 |
–3,2 |
0 |
1,2 |
1,0 |
–1,1 |
Dit niveau LAeq,LT vormt het eindresultaat, d.w.z. het A-gewogen geluidsdrukniveau over lange termijn op het waarneempunt op een bepaald referentietijdsinterval (bijvoorbeeld dag, avond, nacht of een kortere periode tijdens de dag, avond of nacht).
Geometrische divergentie
De demping door geometrische divergentie, Adiv, komt overeen met een vermindering van het geluidsniveau door de voortplantingsafstand. Voor een puntbron in vrij veld wordt de demping in dB verkregen door:
|
Adiv = 20lg(d) + 11 |
(2.5.12) |
waarbij d de rechtstreekse schuine afstand in 3D is tussen de bron en het waarneempunt is.
Atmosferische absorptie
De demping door atmosferische absorptie Aatm tijdens voortplanting over een afstand d wordt verkregen in dB door de vergelijking:
|
Aatm = αatm ∙ d⁄1.000 |
(2.5.13) |
waarbij:
d de rechtstreekse 3D schuine afstand tussen de bron en het waarneempunt is;
αatm de coëfficiënt van atmosferische demping in dB/km op de nominale middenfrequentie voor elke frequentieband is, in overeenstemming met ISO 9613-1.
De waarden van de αatm coëfficiënt worden gegeven voor een temperatuur van 15°C, een relatieve luchtvochtigheid van 70% en een atmosferische druk van 101 325 Pa. Zij worden met de nauwkeurige middenfrequenties van de frequentieband berekend. Deze waarden voldoen aan ISO 9613-1. Het meteorologische gemiddelde op lange termijn wordt gebruikt indien meteorologische gegevens beschikbaar zijn.
|
Octaafband |
αatm [dB/km] |
|---|---|
|
63 |
0,105 |
|
125 |
0,376 |
|
250 |
1,124 |
|
500 |
2,358 |
|
1.000 |
4,079 |
|
2.000 |
8,777 |
|
4.000 |
26,608 |
|
8.000 |
94,962 |
Grondeffect
De demping door het grondeffect is hoofdzakelijk het gevolg van de interferentie tussen het gereflecteerde geluid en het geluid dat zich rechtstreeks van de bron naar het waarneempunt voortplant. Het is fysiek verbonden aan de akoestische absorptie van de grond waarboven de geluidsgolf zich voortplant. Het is echter ook sterk afhankelijk van atmosferische omstandigheden tijdens voortplanting, omdat straalafbuiging de hoogte van het pad boven de grond wijzigt en de effecten van de grond en het land in de buurt van de bron meer of minder versterkt.
In het geval dat de voortplanting tussen de bron en het waarneempunt door een obstakel in het voortplantingsvlak wordt beïnvloed, wordt het grondeffect aan de kant van de bron en het waarneempunt afzonderlijk berekend. In dit geval verwijzen zs en zr naar de equivalente positie van de bron en/of het waarneempunt, zoals aangegeven hieronder waar de berekening van de diffractie Adif wordt gepresenteerd.
Akoestische karakterisering van grond
De akoestische absorptie-eigenschappen van de grond houden voornamelijk verband met zijn porositeit. Compacte grond is in het algemeen reflecterend en poreuze grond is absorberend.
Voor operationele berekeningen wordt de akoestische absorptie van een grond weergegeven met een dimensieloze coëfficiënt G, tussen 0 en 1. G is onafhankelijk van de frequentie. Tabel 2.5.c geeft de G-waarden voor de grond in de openlucht. Het gemiddelde van de coëfficiënt G over een pad krijgt in het algemeen waarden tussen 0 en 1.
|
Beschrijving |
Type |
(kPa • s/m2) |
G-waarde |
|---|---|---|---|
|
Zeer zacht (sneeuw of mosachtig) |
A |
12,5 |
1 |
|
Zachte bosgrond (kort, dicht heideachtig of dik mos) |
B |
31,5 |
1 |
|
Niet-compacte, losse grond (veen, gras, losse aarde) |
C |
80 |
1 |
|
Normale niet-compacte grond (bosbodem, weiden) |
D |
200 |
1 |
|
Compact land en grind (compacte gazons, parkland) |
E |
500 |
0,7 |
|
Compacte dichte grond (grindweg, parkeerplaats) |
F |
2.000 |
0,3 |
|
Harde oppervlakken (veelal normaal asfalt, beton) |
G |
20.000 |
0 |
|
Zeer harde en dichte oppervlakken (dicht asfalt, beton, water) |
H |
200.000 |
0 |
Gpath wordt gedefinieerd als de fractie van absorberende grond die over het gehele pad aanwezig is.
Wanneer de bron en het waarneempunt vlakbij elkaar zijn zodat dp ≤ 30(zs+ zr), is het verschil tussen de grondsoort nabij de bron en de grondsoort nabij het waarneempunt te verwaarlozen. Daarom wordt om met deze opmerking rekening te houden de grondfactor Gpath uiteindelijk als volgt gecorrigeerd:
|
|
(2.5.14) |
waarbij GS de grondfactor van het brongebied is. GS = 0 voor wegdekken1, betonplatenspoor. GS = 1 voor sporen in ballastbed. Er is geen algemeen antwoord in het geval van industriële bronnen en fabrieken.
G kan gerelateerd worden aan de stromingsweerstand.
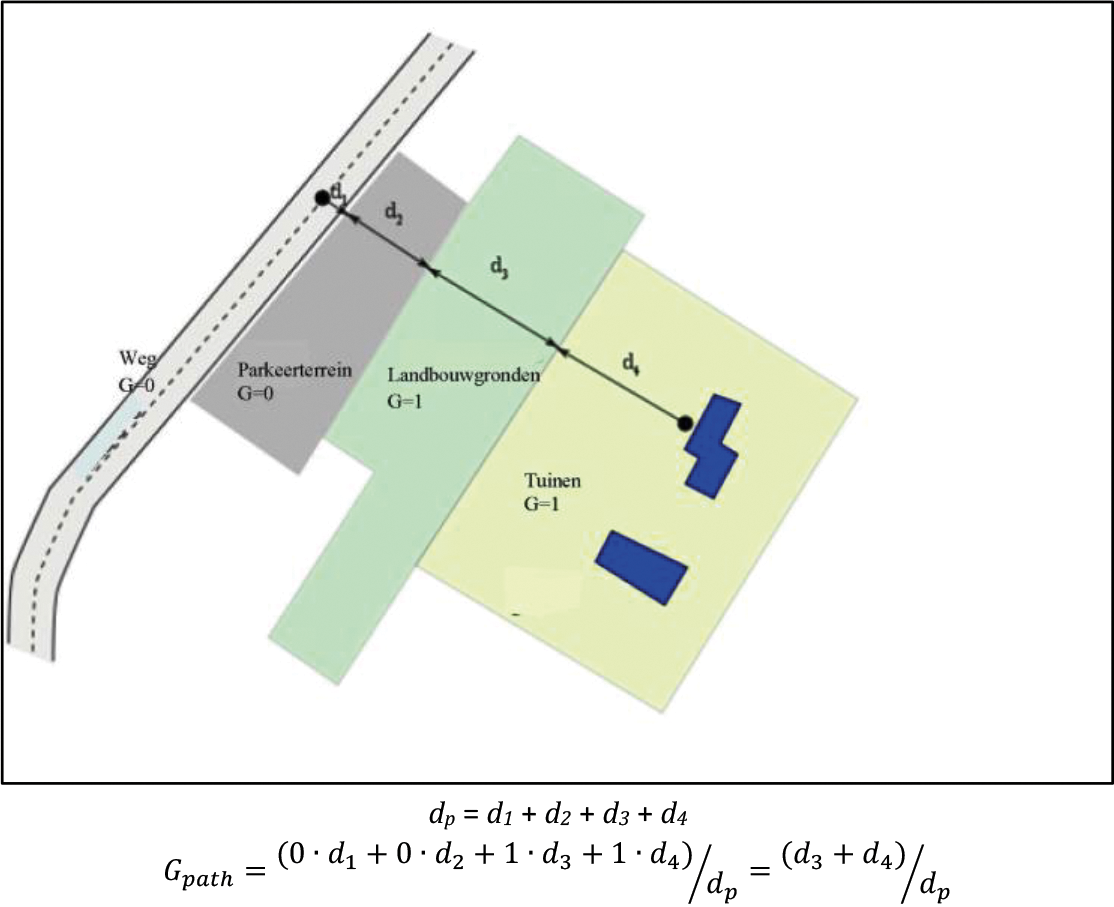
Figuur 2.5.b, Bepaling van de grondcoëfficiënt Gpath over een voortplantingspad
De afstanden dn worden bepaald door een 2D-projectie op het horizontale vlak.
De volgende twee subsecties over berekeningen in homogene
en gunstige omstandigheden introduceren de generieke
![]() en
en
![]() notaties voor de absorptie van de grond. Tabel 2.5.d
geeft het verband tussen deze notaties en de variabelen
Gpath en G’path.
notaties voor de absorptie van de grond. Tabel 2.5.d
geeft het verband tussen deze notaties en de variabelen
Gpath en G’path.

Berekeningen in homogene omstandigheden
De demping door het grondeffect in homogene omstandigheden wordt berekend op basis van de volgende vergelijkingen:
indien G’path ≠ 0
|
|
(2.5.15) |
waarbij
![]()
fm de nominale middenfrequentie is van de frequentieband in kwestie, in Hz, c de snelheid van het geluid in de lucht is, gelijk aan 340 m/s, en Cf wordt bepaald door:
|
|
(2.5.16) |
waarbij de waarden van w worden verkregen door de onderstaande vergelijking:
|
|
(2.5.17) |
![]() kan gelijk zijn aan Gpath of G’path, afhankelijk van het feit of het
grondeffect met of zonder diffractie wordt berekend, en volgens de aard van de
grond onder de bron (werkelijke of afgebogen bron). Dit wordt in de volgende
subsecties vermeld en is in tabel 2.5.d samengevat.
kan gelijk zijn aan Gpath of G’path, afhankelijk van het feit of het
grondeffect met of zonder diffractie wordt berekend, en volgens de aard van de
grond onder de bron (werkelijke of afgebogen bron). Dit wordt in de volgende
subsecties vermeld en is in tabel 2.5.d samengevat.
|
|
(2.5.18) |
is de ondergrens van Aground,H.
Voor een pad (Si,R) in homogene omstandigheden zonder diffractie:
![]() = G’path
= G’path
![]() = G’path
= G’path
Met diffractie, raadpleeg de sectie over diffractie voor de
definities van
![]() en
en
![]() .
.
Indien Gpath = 0: Aground,H = -3 dB
De term
![]() houdt rekening met het feit dat wanneer de bron en
het waarneempunt ver van elkaar liggen, het eerste reflectievlak zich niet
langer op het platform maar op natuurlijke grond bevindt.
houdt rekening met het feit dat wanneer de bron en
het waarneempunt ver van elkaar liggen, het eerste reflectievlak zich niet
langer op het platform maar op natuurlijke grond bevindt.
Berekening in gunstige omstandigheden
Het grondeffect in gunstige omstandigheden wordt berekend met de vergelijking van Aground,H, mits de volgende wijzigingen worden gemaakt:
Indien Gpath ≠ 0
a) In de vergelijking 2.5.15 (Aground,H) worden de hoogten zs en zr vervangen door respectievelijk zs + δzs + δzT en zr + δzr + δzT, waarbij
|
|
(2.5.19) |
a0 = 2 •
10-4 m-1 is het omgekeerde van de kromtestraal
![]()
b) De ondergrens van Aground,F (berekend met ongewijzigde hoogten) is afhankelijk van de geometrie van het pad:
|
|
(2.5.20) |
Indien Gpath = 0: Aground,F = Aground,F,min
De hoogtecorrecties δzs en δzr brengen het effect van de afbuiging van de geluidstralen over. δzT verdisconteert het effect van de turbulentie.
![]() kan ook gelijk zijn aan of Gpath of G’path, afhankelijk van het feit of het
grondeffect met of zonder diffractie wordt berekend, en volgens de aard van de
grond onder de bron (werkelijke of afgebogen bron). Dit wordt in de volgende
subsecties nader bepaald.
kan ook gelijk zijn aan of Gpath of G’path, afhankelijk van het feit of het
grondeffect met of zonder diffractie wordt berekend, en volgens de aard van de
grond onder de bron (werkelijke of afgebogen bron). Dit wordt in de volgende
subsecties nader bepaald.
Voor een pad (Si, R) in gunstige omstandigheden zonder diffractie:
![]() = Gpath in
vergelijking (2.5.17)
= Gpath in
vergelijking (2.5.17)
![]() = G’path
= G’path
Met diffractie, raadpleeg de volgende sectie voor de
definities van
![]() en
en
![]()
Diffractie
Gewoonlijk wordt de diffractie aan de bovenkant van elk obstakel op het voortplantingspad onderzocht. Als het pad ‘hoog genoeg’ over de diffractierand loopt, kan Adif = 0 worden vastgesteld en een rechtstreeks zicht worden berekend, met name door de beoordeling van Aground.
In de praktijk worden de volgende specificaties in aanmerking genomen in het unieke verticale vlak dat zowel de bron als het waarneempunt bevat (een uitvouwend Chinees kamerscherm in het geval van een traject met reflecties). De rechtstreekse straal van de bron naar het waarneempunt is een rechte lijn onder homogene voortplantingscondities en een gebogen lijn (boog waarvan de straal afhankelijk is van de lengte van de rechtstreekse straal) onder gunstige voortplantingscondities.
Als de rechtstreekse straal niet is geblokkeerd, wordt de rand D gezocht die het grootste padverschil δ oplevert (de kleinste absolute waarde, omdat deze padverschillen negatief zijn). Diffractie wordt in aanmerking genomen als
− dit padverschil groter is dan -λ/20; en
− als aan het ‘Rayleigh criterium’ is voldaan.
Dit is het geval als δ groter is dan λ/4 – δ*, waarbij δ* het padverschil is dat met deze zelfde rand D is berekend, maar gerelateerd is aan de gespiegelde bron S* berekend met het gemiddelde grondvlak aan de bronkant en aan het gespiegelde waarneempunt R* berekend met het gemiddelde grondvlak aan de waarneemkant. Om δ* te berekenen worden alleen de punten S*, D en R* in aanmerking genomen – andere randen die het pad S*->D->R* blokkeren, worden verwaarloosd. Voor de bovenstaande overwegingen wordt de golflengte λ berekend met behulp van de nominale middenfrequentie en een geluidssnelheid van 340 m/s.
Als aan deze twee voorwaarden is voldaan, wordt de bronkant door rand D van de waarneemkant gescheiden, worden twee afzonderlijke gemiddelde grondvlakken berekend en wordt Adif berekend zoals beschreven in de rest van dit deel. Anders wordt voor dit pad geen demping door diffractie overwogen, wordt een gemeenschappelijk gemiddeld grondvlak voor het pad S -> R berekend, en Aground zonder diffractie (Adif = 0 dB) berekend. Deze regel geldt zowel in homogene als in gunstige omstandigheden.
Wanneer voor een specifieke frequentieband een berekening volgens de in deze sectie beschreven procedure wordt gemaakt, wordt Aground vastgesteld als gelijk te zijn aan 0 dB voor de berekening van de totale demping. Het grondeffect wordt rechtstreeks in de vergelijking van de algemene diffractieberekening in aanmerking genomen.
De hier voorgestelde vergelijkingen worden gebruikt om de diffractie op dunne schermen, dikke schermen, gebouwen, bermen (natuurlijke of kunstmatige) en door de randen van dijken, ingravingen en viaducten te verwerken.
Wanneer verscheidene diffractie-obstakels op een voortplantingspad worden aangetroffen, worden ze behandeld als een meervoudige diffractie door toepassing van de procedure die in de volgende sectie over de berekening van het padverschil wordt beschreven.
De hier gepresenteerde procedures worden voor de berekening van dempingen in zowel homogene als gunstige omstandigheden gebruikt. Bij de berekening van het padverschil en voor de berekening van de grondeffecten voor en na diffractie wordt rekening gehouden met straalbuiging.
Algemene beginslen
Figuur 2.5.c illustreert de algemene methode voor berekening van de demping door diffractie. Deze methode is gebaseerd op het opsplitsen van het voortplantingspad in twee delen: het pad van de ‘bronkant’, gelegen tussen de bron en het diffractiepunt, en het pad van ‘waarneemkant’, gelegen tussen het diffractiepunt en het waarneempunt.
Het volgende wordt berekend:
• een grondeffect, bronkant, Δground(S,O)
• een grondeffect, waarneemkant, Δground(O,R)
• en drie diffracties:
• tussen de bron S en het waarneempunt R: Δdif(S,R)
• tussen de spiegelbron S′ en R: Δdif(S′,R)
• tussen S en de spiegelontvanger R′: Δdif(S,R′).
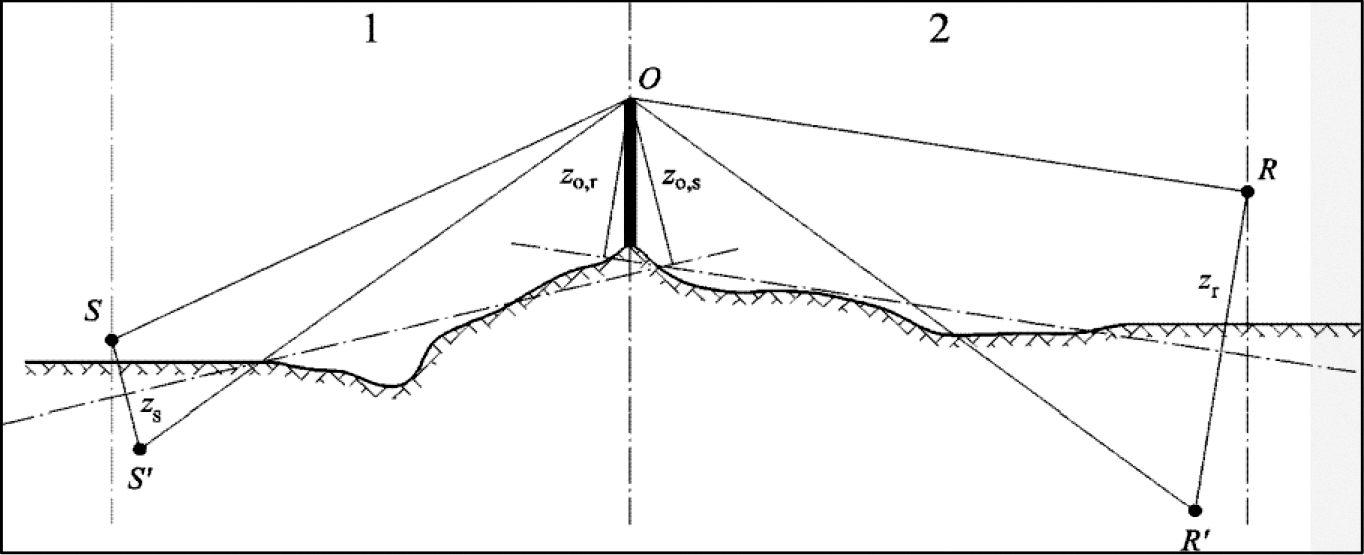
Figuur 2.5.c, Geometrie van een berekening van de demping door diffractie
1: Bronkant
2: Waarneemkant
waarbij:
S de bron is;
R het waarneempunt is;
S’ de spiegelbron is in verhouding tot het gemiddelde grondvlak aan de bronkant;
R’ de spiegelontvanger is in verhouding tot het gemiddelde grondvlak aan de waarneemkant;
O het diffractiepunt is;
zs de equivalente hoogte is van de bron S in verhouding tot het gemiddelde vlak aan de bronkant;
zo,s de equivalente hoogte is van het diffractiepunt O in verhouding tot het gemiddelde grondvlak aan de bronkant;
zr de equivalente hoogte is van het waarneempunt R in verhouding tot het gemiddelde vlak aan de waarneemkant;
zo,r de equivalente hoogte is van het diffractiepunt O in verhouding tot het gemiddelde grondvlak aan de waarneemkant.
De onregelmatigheid van de grond tussen de bron en het diffractiepunt en tussen het diffractiepunt en het waarneempunt wordt in aanmerking genomen door middel van equivalente hoogten berekend in verhouding tot het gemiddelde grondvlak, eerst de bronkant en vervolgens de waarneemkant (twee gemiddelde grondvlakken), volgens de methode beschreven in de subsectie over aanmerkelijke hoogten boven de grond (figuur 2.5.a).
Zuivere diffractie
Voor zuivere diffractie, zonder grondeffecten, wordt de demping verkregen door:
|
|
(2.5.21) |
|
waarbij:
λ de golflengte is op de nominale middenfrequentie van de frequentieband in kwestie;
δ het padverschil is tussen het gebogen pad en het rechtstreekse pad (zie de volgende subsectie over de berekening van het padverschil);
C’’ coëfficiënt is die wordt gebruikt om rekening te houden met meervoudige diffracties:
C’’ = 1 voor een enkele diffractie.
Voor meervoudige diffractie, indien e de totale afstand langs het pad is tussen het eerste en het laatste diffractiepunt (gebruik bij gunstige omstandigheden gebogen stralen) en als e hoger is dan 0,3 m (anders geldt C’’ = 1), wordt deze coëfficiënt gedefinieerd door:
|
|
(2.5.22) |
De waarden van ∆dif worden vastgelegd:
• indien ∆dif < 0: ∆dif = 0 dB
• indien ∆dif > 25: ∆dif = 25 dB voor een diffractie op een horizontale rand en alleen op de term ∆dif die in de berekening van Adifvoorkomt. Deze bovengrens wordt niet toegepast in de ∆dif-termen die in de berekening van ∆ground gebruikt worden, of voor een diffractie op een verticale rand (laterale diffractie) in het geval van kartering van industrielawaai.
Berekening van het padverschil
Het padverschil δ wordt berekend in een verticaal vlak dat de bron en het waarneempunt bevat. Dit is een benadering met betrekking tot het beginsel van Fermat. De benadering blijft hier van toepassing (bronlijnen). Het padverschil δ wordt zoals in de volgende figuren berekend, op basis van de aangetroffen situaties.
Homogene omstandigheden
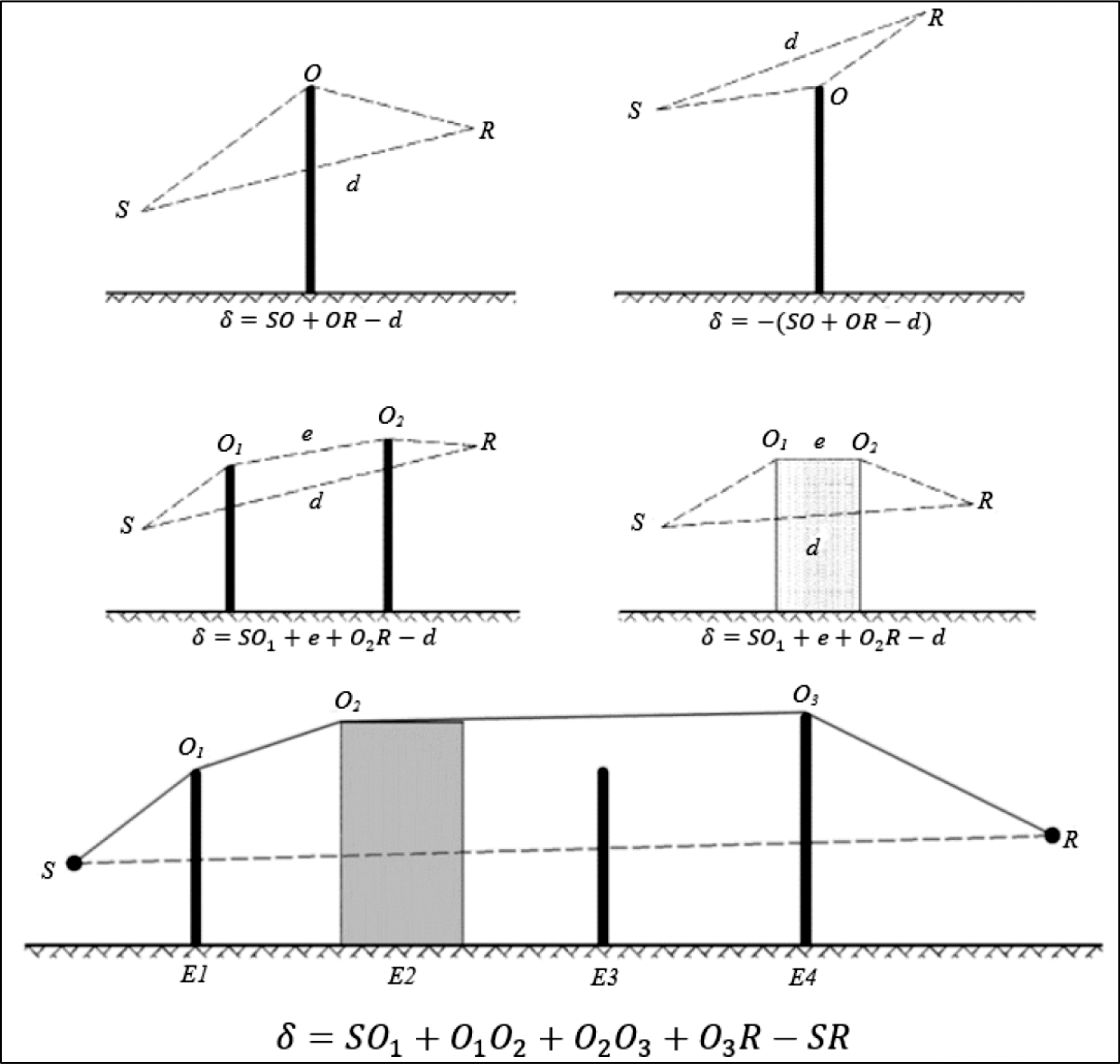
Figuur 2.5.d, Berekening van het padverschil in homogene omstandigheden. O, O1, O2 en O3 zijn de diffractiepunten
Opmerking: voor elke configuratie wordt de uitdrukking van δ gegeven.
Gunstige omstandigheden
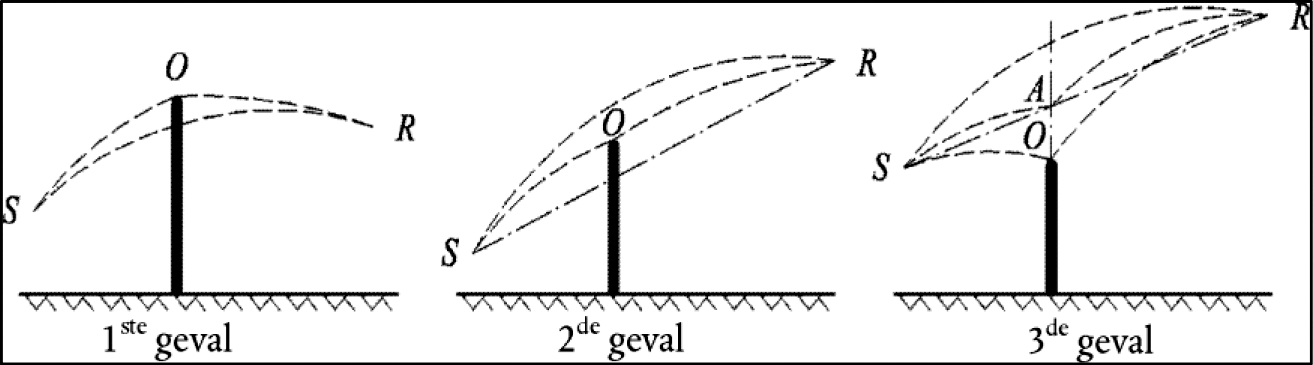
Figuur 2.5.e, Berekening van het padverschil in gunstige omstandigheden (enkele diffractie)
In gunstige omstandigheden hebben de drie gebogen geluidsstralen SO, OR en SR een identieke kromtestraal Γ, gedefinieerd door:
|
Γ = max(1.000,8d) |
(2.5.23) |
Waarbij d wordt gedefinieerd door de 3D-afstand tussen de bron en het waarneempunt van het opengevouwen pad.
De lengte van de kromming van een geluidsstraal
![]() wordt in gunstige omstandigheden aangeduid als
wordt in gunstige omstandigheden aangeduid als
![]() Deze lengte is gelijk aan:
Deze lengte is gelijk aan:
|
|
(2.5.24) |
In beginsel dienen drie scenario's in aanmerking te worden genomen in de berekening van het padverschil in gunstige omstandigheden δF (zie figuur 2.5.e). In de praktijk volstaan twee vergelijkingen:
als de rechte geluidstraal SR door het obstakel (1e en 2e geval in figuur 2.5.e) wordt gemaskeerd:
|
|
(2.5.25) |
als de rechte geluidstraal SR niet door het obstakel (3e geval in figuur 2.5.e) wordt gemaskeerd:
|
|
(2.5.26) |
waarbij A het snijpunt van de rechte geluidstraal SR en het verlengde van het diffractie veroorzakende obstakel is.
Voor de meervoudige diffracties in gunstige omstandigheden:
• bepaal het convexe omhulsel gedefinieerd door de verschillende mogelijke diffractieranden;
• elimineer de diffractieranden die zich niet op de grens van het convexe omhulsel bevinden;
• bereken δF op basis van de lengten van de gebogen geluidsstraal door het gebogen pad in net zo veel gebogen segmenten te verdelen als er nodig zijn (zie figuur 2.5.f)
|
|
(2.5.27) |
Onder gunstige omstandigheden bestaat het voortplantingspad in het verticale voortplantingsvlak altijd uit segmenten van een cirkel waarvan de straal wordt verkregen door de 3D-afstand tussen de bron en het waarneempunt, d.w.z. alle segmenten van een voortplantingspad hebben dezelfde kromtestraal. Als de directe-boogverbinding tussen de bron en het waarneempunt geblokkeerd is, wordt het voortplantingspad gedefinieerd als de kortste convexe combinatie van bogen die alle obstakels omhult. Convex betekent in dit verband dat op elk diffractiepunt het uitgaande straalsegment naar beneden wordt afgebogen ten opzichte van het inkomende straalsegment.
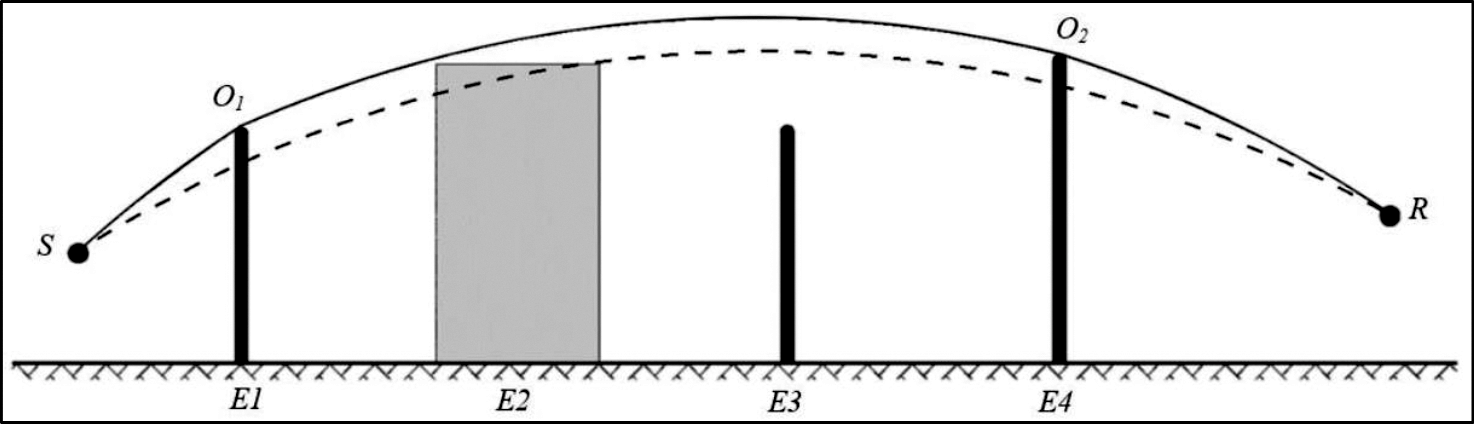
Figuur 2.5.f, Voorbeeld van berekening van het padverschil in gunstige omstandigheden, in het geval van meervoudige diffracties
In het scenario dat in figuur 2.5.f wordt afgebeeld is het padverschil:
|
|
(2.5.28) |
Berekening van de demping Adif
De demping door diffractie, waarbij de grondeffecten aan de bronkant en waarneemkant in aanmerking worden genomen, wordt berekend op basis van de volgende algemene vergelijkingen:
|
Adif = ∆dif(S.R) + ∆ground (S,O) + ∆ground(On,R) |
(2.5.29) |
waarbij:
• ∆dif(S,R) de demping is door de diffractie tussen de bron S en het waarneempunt R,
• ∆ground(S,O) de demping is door het grondeffect aan de bronkant, gewogen door de diffractie aan de bronkant. Daarbij wordt er van uitgegaan dat O = O1 in het geval van meervoudige diffracties zoals in figuur 2.5.f,
• ∆ground(On,R) de demping is door het grondeffect aan de waarneemkant, gewogen door de diffractie aan de waarneemkant (zie de volgende subsectie over de berekening van de term ∆ground(On,R)).
Berekening van de term ∆ground(S,O)
|
|
(2.5.30) |
waarbij:
• Aground(S,O) de demping is door het grondeffect tussen de bron S en het diffractiepunt O. Deze term wordt berekend zoals aangegeven in de vorige subsectie over berekeningen in homogene omstandigheden en in de vorige subsectie over berekening in gunstige omstandigheden, met de volgende hypothesen:
• zr = zo,s,
• Gpath tussen S en O wordt berekend,
• In homogene omstandigheden:
![]() = G'path in
vergelijking (2.5.17),
= G'path in
vergelijking (2.5.17),
![]() = G'path in
vergelijking (2.5.18),
= G'path in
vergelijking (2.5.18),
• In gunstige omstandigheden:
![]() = Gpath in
vergelijking (2.5.17),
= Gpath in
vergelijking (2.5.17),
![]() = G'path in
vergelijking (2.5.20),
= G'path in
vergelijking (2.5.20),
• ∆dif(S’,R) is de demping door de diffractie tussen de spiegelbron S′ en R, berekend als in de vorige subsectie over zuivere diffractie,
• ∆dif(S,R) is de demping door de diffractie tussen S en R, berekend als in de vorige subsectie over zuivere diffractie.
In het bijzondere geval dat de bron onder het gemiddelde grondvlak ligt:
∆dif(S’,R) = ∆dif(S,R) en ∆ground(S,O) = Aground(S,O).
Berekening van de term ∆ground(O,R)
|
|
(2.5.31) |
waarbij:
• Aground(O,R) de demping is door het grondeffect tussen het diffractiepunt O en het waarneempunt R. Deze term wordt berekend zoals aangegeven in de vorige subsectie over berekening in homogene omstandigheden en in de vorige subsectie over berekening in gunstige omstandigheden, met de volgende hypothesen:
• zs = zo,r,
• Gpath wordt berekend tussen O en R,
De correctie G’path hoeft hier niet in aanmerking te worden genomen omdat de bron in kwestie het diffractiepunt is. Daarom wordt Gpath wel in de berekening van grondeffecten gebruikt, inclusief voor de ondergrensterm van de vergelijking die dan -3(1 – Gpath) wordt.
– In homogene omstandigheden:
![]() in vergelijking (2.5.17),
in vergelijking (2.5.17),
![]() in vergelijking (2.5.18),
in vergelijking (2.5.18),
– In gunstige omstandigheden:
![]() in vergelijking (2.5.17),
in vergelijking (2.5.17),
![]() in vergelijking (2.5.20),
in vergelijking (2.5.20),
− ∆dif(S,R’) is de demping door de diffractie tussen S en de spiegelontvanger R’, berekend als in de vorige subsectie over zuivere diffractie;
− ∆dif(S,R) is de demping door de diffractie tussen S en R, berekend als in de vorige subsectie over zuivere diffractie.
In het bijzondere geval dat het waarneempunt onder het gemiddelde grondvlak ligt: ∆dif(S,R’) = ∆dif(S,R) en ∆ground(O,R) = Aground(O,R).
Scenario's met verticale rand
Vergelijking (2.5.21) kan worden gebruikt voor de berekening van de diffracties op verticale randen (laterale diffracties) in het geval van industrielawaai. In dit geval wordt Adif = ∆dif(S,R) weggenomen en blijft de term Aground behouden. Bovendien worden Aatm en Aground berekend op basis van de totale lengte van het voortplantingspad. Adiv wordt nog steeds berekend vanaf de rechtstreekse afstand d. De vergelijkingen (2.5.8) en (2.5.6) worden respectievelijk:
|
|
(2.5.32) |
|
|
|
(2.5.33) |
Laterale diffractie wordt alleen in aanmerking genomen in gevallen waarin aan de volgende voorwaarden wordt voldaan:
• De bron is een echte puntbron – niet geproduceerd door segmentatie van een uitgebreide bron zoals een bronlijn of diffuse bron.
• De bron is geen gespiegelde bron die is geconstrueerd om een reflectie te berekenen.
• De rechtstreekse straal tussen de bron en het waarneempunt ligt volledig boven het terreinprofiel.
• In het verticale vlak met S en R is het padverschil δ groter dan 0, d.w.z. de rechtstreekse straal wordt geblokkeerd. Daarom kan in sommige situaties laterale diffractie in aanmerking worden genomen onder homogene voortplantingscondities, maar niet onder gunstige voortplantingscondities.
Als aan al deze voorwaarden is voldaan, wordt naast het gebogen voortplantingspad in het verticale vlak met de bron en het waarneempunt rekening gehouden met maximaal twee lateraal gebogen voortplantingspaden. Het laterale vlak is gedefinieerd als het vlak dat loodrecht staat op het verticale vlak en ook de bron en het waarneempunt bevat. De snijvlakken met dit laterale vlak zijn opgebouwd uit alle obstakels die door de rechtstreekse straal van de bron naar het waarneempunt worden doorsneden. In het laterale vlak bepaalt de kortste convexe verbinding tussen de bron en het waarneempunt, bestaande uit rechtlijnige segmenten en die deze snijvlakken omvat, de verticale randen die in aanmerking worden genomen bij de constructie van het lateraal gebogen voortplantingspad.
Om de demping door het grondeffect voor een lateraal gebogen voortplantingspad te berekenen, wordt het gemiddelde grondvlak tussen de bron en het waarneempunt berekend, rekening houdend met het grondprofiel dat verticaal onder het voortplantingspad ligt. Als in de projectie op een horizontaal vlak een lateraal voortplantingspad de projectie van een gebouw doorsnijdt, wordt dit in aanmerking genomen in de berekening van Gpath (meestal met G = 0) en in de berekening van het gemiddelde grondvlak met de verticale hoogte van het gebouw.
Reflecties op verticale obstakels
Demping door absorptie
De reflecties op verticale obstakels worden door middel van spiegelbronnen behandeld. Reflecties op gevels van gebouwen en geluidweringen worden dus op deze wijze behandeld.
Oppervlakken van objecten worden alleen als reflecterend beschouwd als ze minder dan 15° aflopen in verhouding tot de verticaal. Reflecties worden alleen in aanmerking genomen voor paden in het verticale voortplantingsvlak, dus niet voor lateraal gebogen paden. Voor de invallende en gereflecteerde paden, en in de veronderstelling dat het reflecterend oppervlak verticaal is, wordt het punt van reflectie (dat op het reflecterende object ligt) geconstrueerd met behulp van rechte lijnen onder homogene, en gebogen lijnen onder gunstige voortplantingscondities. De hoogte van het reflecterende object moet, gemeten door het punt van reflectie en gezien vanuit de richting van de invallende straal, ten minste 0,5 m bedragen. Na projectie op een horizontaal vlak moet de breedte van het reflecterend object, gemeten door het punt van reflectie en gezien vanuit de richting van de invallende straal, ten minste 0,5 m bedragen.
NB: reflecties op de grond worden hier niet behandeld. Deze worden bij de berekeningen van demping door de grens (grond, diffractie) in aanmerking genomen.
Als LWS het vermogensniveau van de bron S is, en αr de absorptiecoëfficiënt van het oppervlak van het obstakel is zoals gedefinieerd door EN1793-1:2013, dan is het vermogensniveau van de spiegelbron S’ gelijk aan:
|
LWS' = LWS + 10 ∙ lg(1-αr) = LWS + Arefl |
(2.5.34) |
waarbij 0 ≤ αr < 1
De hierboven beschreven voortplantingsdempingen worden dan
op dit pad (spiegelbron, waarneempunt) als voor een rechtstreeks pad toegepast.
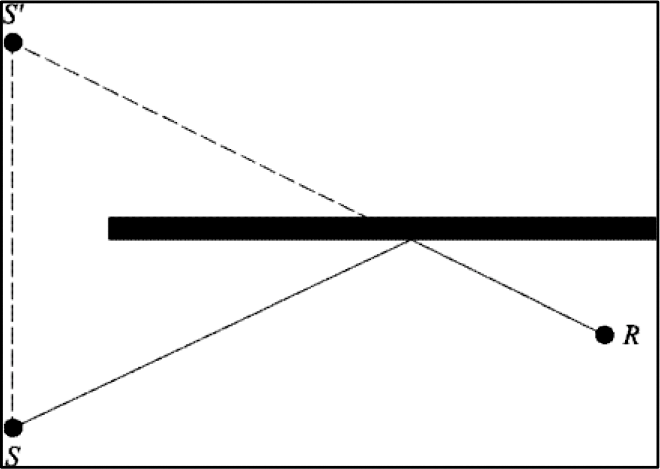
Figuur 2.5.g, Spiegelende reflecties op een obstakel behandeld volgens de spiegelbronmethode (S: bron, S′: spiegelbron, R: waarneempunt)
Demping door retro-diffractie
In het geometrische onderzoek van geluidspaden hangt het aandeel van de energie dat door een verticaal obstakel (muur, gebouw) wordt gereflecteerd af van de afstand van het punt waar de straal aankomt tot de bovenste rand van het obstakel. Dit verlies van akoestische energie wanneer de straal wordt gereflecteerd, wordt demping door retro-diffractie genoemd.
In het geval van mogelijk meerdere reflecties tussen twee verticale wanden wordt ten minste de eerste reflectie in aanmerking genomen.
Bij een open tunnelbak (zie bijvoorbeeld figuur 2.5.h)
wordt de demping door retro-diffractie toegepast op elke reflectie op de
steunmuren.
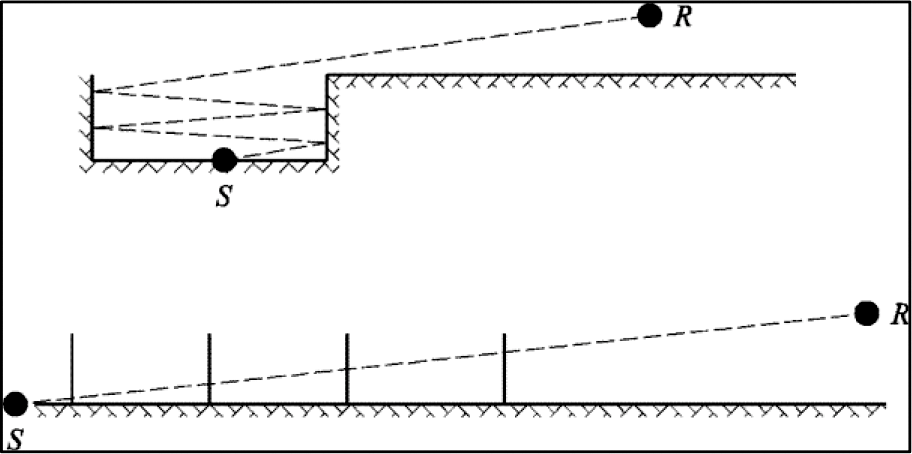
Figuur 2.5.h, Geluidsstraal die vier keer in een baan in een open tunnelbak wordt gereflecteerd: werkelijk dwarsprofiel (boven), opengevouwen dwarsdoorsnede (onder)
In deze afbeelding bereikt de geluidsstraal het waarneempunt ‘door achtereenvolgens door de steunmuren van de open tunnelbak te gaan’, die daarom met openingen kunnen worden vergeleken.
Bij de berekening van voortplanting door een opening is het geluidsveld op het waarneempunt de som van het directe veld en het door de randen van de opening gediffracteerde veld. Dit gediffracteerde veld zorgt voor de continuïteit van de overgang tussen het gebied met direct zicht en het schaduw gebied. Wanneer de straal de rand van de opening nadert, wordt het directe veld gedempt. De berekening is identiek aan die van de demping door een geluidsscherm in het vrije gebied.
Het padverschil δ’ in verband met elke retro-diffractie is het tegenovergestelde van het padverschil tussen S en R relatief op elke bovenrand O, en dit in een weergave volgens een ingezette dwarsdoorsnede (zie figuur 2.5.i).
|
δ' = – (SO + OR – SR) |
(2.5.35) |

Figuur 2.5.i, Het padverschil voor de tweede reflectie
Het ‘min’-teken van vergelijking (2.5.35) betekent dat het waarneempunt hier in het gebied met direct zicht in aanmerking wordt genomen.
Demping via retro-diffractie ∆retrodif wordt verkregen met behulp van vergelijking (2.5.36), die lijkt op vergelijking (2.5.21) met bewerkte notaties.
|
|
(2.5.36) |
Deze demping wordt toegepast op de rechtstreekse straal telkens wanneer die ‘door’ een muur of gebouw gaat (reflecteert). Het vermogensniveau van de spiegelbron S’ wordt dus:
|
LW' = LW + 10lg(1 – αr) – ∆retrodif |
(2.5.37) |
In complexe voortplantingsconfiguraties kunnen diffracties
tussen reflecties of tussen het waarneempunt en de reflecties bestaan. In dit
geval wordt de retro-diffractie door de wanden geschat door het pad tussen de
bron en het eerste diffractiepunt R’ (dat derhalve in vergelijking (2.5.35) als
het waarneempunt wordt beschouwd) in aanmerking te nemen. Dit beginsel wordt
weergegeven in figuur 2.5.j.
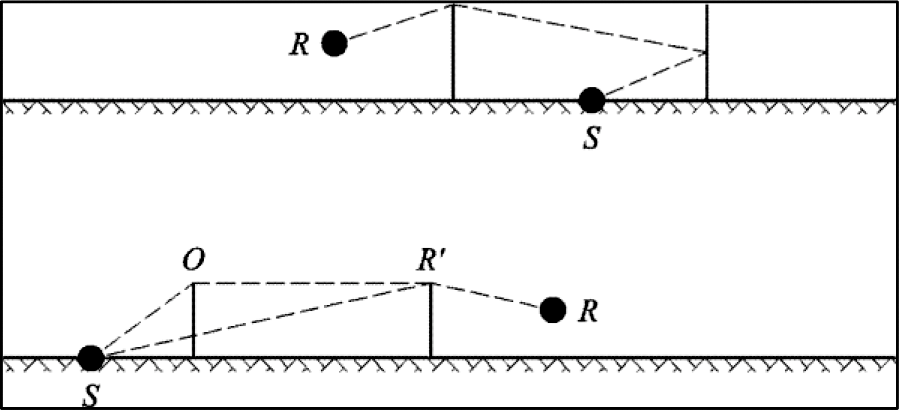
Figuur 2.5.j, Het padverschil in de aanwezigheid van een diffractie: werkelijke dwarsdoorsnede (boven), opengevouwen dwarsdoorsnede (onder)
In het geval van meerdere reflecties worden de reflecties door elke individuele reflectie toegevoegd.
Wanneer er een reflecterend geluidscherm of reflecterend obstakel in de buurt van het spoor is, worden de geluidsstralen van de bron achtereenvolgens gereflecteerd door dit obstakel en door het zijvlak van het spoorvoertuig. Onder deze omstandigheden gaan de geluidsstralen tussen het obstakel en de carrosserie van het spoorvoertuig door voordat ze van de bovenrand van het obstakel worden afgebogen.
Om rekening te houden met meerdere reflecties tussen een spoorwegvoertuig en een nabijgelegen obstakel, wordt het geluidsvermogen van een enkele equivalente bron berekend. In deze berekening worden grondeffecten genegeerd.
Voor het afleiden van het geluidsvermogen van de equivalente bron gelden de volgende definities:
• De oorsprong van het coördinatensysteem is de linker railkop
• Een echte bron bevindt zich op S (ds=0, hs), waarbij hs de hoogte van de bron ten opzichte van de railkop is
• Het vlak h=0 definieert de carrosserie van het voertuig
• Een verticaal obstakel met de bovenkant bij B (dB, hb)
• Een waarneempunt dat zich bevindt op een afstand dR > 0 achter het obstakel waar R de coördinaten (dB+dR, hR) heeft
De binnenzijde van het obstakel heeft absorptiecoëfficiënten α(f) per octaafband. De carrosserie van het spoorvoertuig heeft een equivalente reflectiecoëfficiënt Cref. Normaal gesproken is Cref gelijk aan 1. Alleen in het geval van open, platte goederenwagons kan een waarde van 0 worden gebruikt. Als dB>5hB of α(f) > 0,8 is, wordt er geen rekening gehouden met de interactie van de trein en het scherm.
In deze configuratie kunnen meerdere reflecties tussen de
carrosserie van het spoorvoertuig en het obstakel worden berekend met behulp
van spiegelbronnen die zich op Sn(dn =
-2n • dB, hn = hs),
n=0,1,2,..N bevinden; zoals weergegeven in figuur 2.5.k.
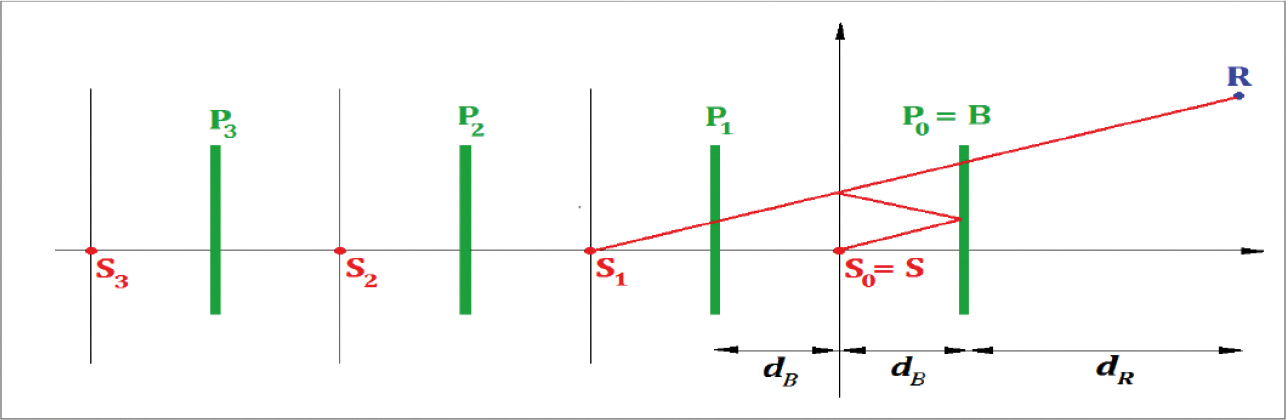
figuur 2.5.k. Weergave van de modellering meervoudige reflecties tussen trein en geluidscherm.
Het geluidsvermogen van de equivalente bron wordt uitgedrukt door:
|
|
(2.5.38) |
Waar het geluidsvermogen van de gedeeltelijke bronnen wordt verkregen door:
|
LW,n = LW + ∆Lgeo,n + ∆Ldif,n + ∆Labs,n + ∆Lref,n + ∆Lretrodif,n |
(2.5.39) |
Met:
|
LW |
het geluidsvermogen van de echte bron |
|
∆Lgeo,n |
een correctieterm voor geometrische uitbreiding |
|
∆Ldif,n |
een correctieterm voor diffractie door de bovenkant van het obstakel |
|
∆Labs,n |
een correctieterm voor de absorptie aan de binnenzijde van het obstakel |
|
∆Lref,n |
een correctieterm voor de reflectie van de carrosserie van het spoorvoertuig |
|
∆Lretrodif,n |
een correctieterm voor de eindige hoogte van het obstakel als een reflecterend object |
De correctie voor geometrische uitbreiding wordt verkregen door
|
|
(2.5.40) |
|
|
(2.5.41) |
De correctie voor diffractie door de bovenkant van het obstakel wordt verkregen door (2.5.42):
|
∆Ldif,n = D0 – Dn |
(2.5.42) |
Waarbij Dn de demping door diffractie is, berekend met formule (2.5.21) waarin C’’ = 1 voor het pad dat de bron Sn verbindt met het waarneempunt R, rekening houdend met diffractie aan de bovenkant van het obstakel B:
|
δn = ± (| Sn B | + | BR | – | Sn R |) |
(2.5.43) |
De correctie voor absorptie aan de binnenzijde van het obstakel wordt verkregen door:
|
∆Labs,n = 10 ∙ n ∙ lg(1 – α) |
(2.5.44) |
De correctie voor de reflectie van de carrosserie van het spoorvoertuig wordt verkregen door:
|
∆Lref,n = 10 ∙ n ∙ lg ((Cref) |
(2.5.45) |
De correctie voor de eindige hoogte van het reflecterend obstakel wordt door middel van retro-diffractie in aanmerking genomen. Het straalpad dat overeenkomt met een afbeelding in de orde van N > 0 wordt n maal gereflecteerd door het obstakel. In de dwarsdoorsnede vinden deze reflecties plaats op de afstanden di = –(2i – q)db, i = 1,2,..n. Met Pi (d = di, h = hb), i = 1,2,..n als de bovenkant van deze reflecterende oppervlakken. Op elk van deze punten wordt een correctieterm berekend als:
|
|
(2.5.46) |
Waarbij ∆Lretrodif,n,i wordt berekend voor een bron op positie Sn, de bovenkant van een obstakel op Pi en een waarneempunt op positie R'. De positie van het equivalente waarneempunt R' wordt verkregen door R'=R als het waarneempunt zich boven de zichtlijn van Sn van naar B bevindt; anders wordt de positie van het equivalente waarneempunt ingenomen op de zichtlijn verticaal boven het echte waarneempunt; dat zijn
|
dR' = dR |
(2.5.47) |
|
|
(2.5.48) |
Bepaling van het aan lawaai blootgestelde gebied
De beoordeling van het aan lawaai blootgestelde gebied is gebaseerd op geluidsbeoordelingspunten op 4 m ± 0,2 m boven de grond, die overeenkomen met de in hoofdstuk 2.5 gedefinieerde waarneempunten, berekend op een raster voor afzonderlijke bronnen.
Voor de rasterpunten die zich binnen een gebouw bevinden wordt een geluidniveau toegekend dat gelijk is aan dat van de stilste nabijgelegen geluidswaarneempunt buiten dat gebouw.
Afhankelijk van de rasterresolutie wordt aan elk berekeningspunt in het raster het bijbehorende oppervlak toegewezen. Bijvoorbeeld, met een raster van 10 m x 10 m vertegenwoordigt elk beoordelingspunt een oppervlakte van 100 vierkante meter die wordt blootgesteld aan het berekende geluidsniveau.
Toewijzing van geluidsbeoordelingspunten aan gebouwen die geen woningen bevatten
De beoordeling van de blootstelling aan lawaai van gebouwen die geen woningen bevatten, zoals scholen en ziekenhuizen, is gebaseerd op geluidsbeoordelingspunten op 4 m ± 0,2 m boven de grond, die overeenkomen met de in 2.5 bepaalde waarneempunten.
Voor de beoordeling van gebouwen die geen woningen bevatten worden de waarneempunten op ongeveer 0,1 m vóór de gevels van de gebouwen geplaatst. Reflecties van de desbetreffende gevel wordt bij de berekening buiten beschouwing gelaten. Het gebouw wordt vervolgens in verband gebracht met het waarneempunt op de gevels met de hoogste geluidsbelasting.
Bepaling van de geluidsbelasting waaraan woningen en bewoners worden blootgesteld
Voor de beoordeling van geluidsbelasting van de bevolking worden alleen woongebouwen in aanmerking genomen. Er worden geen personen toegewezen aan andere gebouwen die niet als woning worden gebruikt, zoals scholen, ziekenhuizen, kantoorgebouwen of fabrieken.
Bepaling van het aantal inwoners van een gebouw
Het aantal inwoners per wooneenheid is gelijk aan de ‘gemiddelde huishoudensgrootte’ volgens de meest recente publicatie van het Centraal Bureau voor de Statistiek (CBS). Het aantal inwoners per gebouw is de som van het aantal inwoners van alle wooneenheden in het gebouw.
Toewijzing van geluidsbeoordelingspunten aan woningen en bewoners
De beoordeling van de blootstelling aan geluidsbelasting van woningen en bewoners is gebaseerd op geluidsbeoordelingspunten op 4 m ± 0,2 m boven de grond, die overeenkomen met de in hoofdstuk 2.5, gedefinieerde waarneempunten.
Om voor de geluidsbronnen wegen, spoorwegen en industrie het aantal woningen en bewoners te berekenen, worden waarneempunten op ongeveer 0,1 m vóór de gevels van woongebouwen geplaatst. Reflecties van de desbetreffende gevel worden bij de berekening buiten beschouwing gelaten. Voor het plaatsen van de waarneempunten wordt een van de onderstaande twee procedures gebruikt.
Geval 1: gevels die in regelmatige intervallen zijn verdeeld
op elke gevel
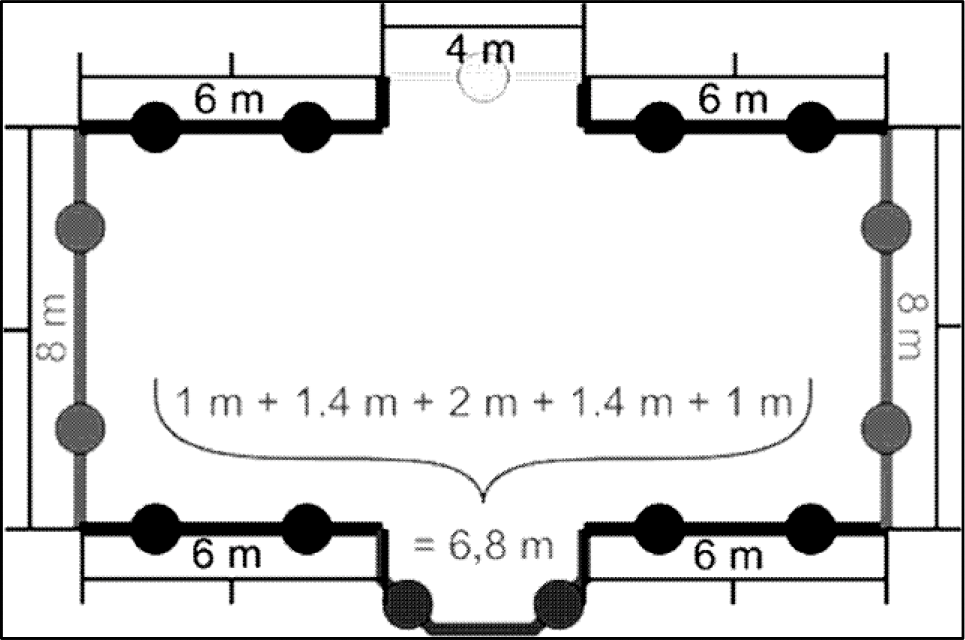
Figuur 2.6.a, Voorbeeld van waarneemlocaties in de omgeving van een gebouw volgens de geval-1-procedure
a) Segmenten van meer dan 5 m lengte worden verdeeld in regelmatige intervallen met de langst mogelijke lengte, maar minder dan of gelijk aan 5 m. Waarneempunten worden in het midden van elk regelmatig interval geplaatst.
b) Overige segmenten van meer dan 2,5 m lengte worden door één waarneempunt in het midden van elk segment weergegeven.
c) Overige aangrenzende segmenten met een totale lengte van meer dan 5 m worden als polylijn-objecten behandeld op een wijze die vergelijkbaar is met die welke in a) en b) wordt beschreven.
Geval 2: gevels op vaste afstand verdeeld van het begin van
de veelhoek
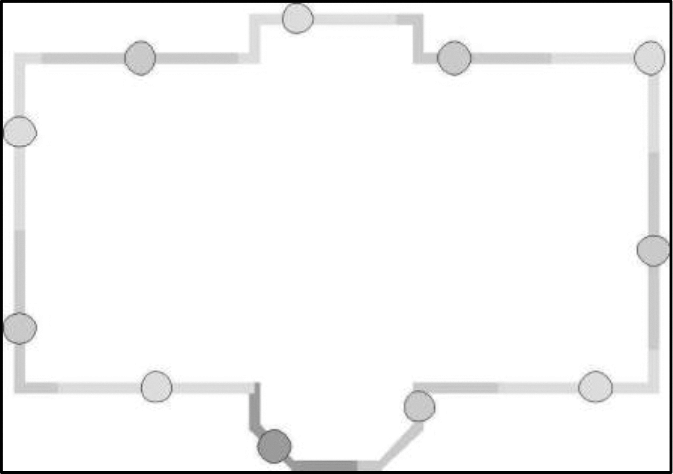
Figuur 2.6.b, Voorbeeld van waarneemlocaties in de omgeving van een gebouw volgens de geval-2-procedure
a) Gevels worden afzonderlijk beschouwd of vanaf de startpositie om de 5 m verdeeld, waarbij een waarneempositie halverwege de gevel of het 5 m-segment wordt geplaatst.
b) Het waarneempunt van het resterende deel bevindt zich in het middelpunt.
Toewijzing van woningen en bewoners aan waarneempunten
Wanneer informatie over de locatie van woningen binnen de voetafdruk van het gebouw beschikbaar is, worden die woningen en bewoners toegewezen aan het waarneempunt op de meest blootgestelde gevel van die woning. Het kan hierbij bijvoorbeeld gaan om vrijstaande woningen, twee-onder-een-kap- en terraswoningen, of flatgebouwen, waarbij de interne indeling van het gebouw bekend is, of voor gebouwen met een vloeroppervlakte die een enkele woning per verdieping aangeeft, of voor gebouwen met een vloeroppervlakte en -hoogte die een enkele woning per gebouw aangeeft.
Wanneer er geen informatie beschikbaar is over de locatie van woningen binnen de voetafdruk van het gebouw, zoals hierboven uitgelegd, wordt een van de twee volgende methoden gebruikt om per gebouw de blootstelling aan lawaai van de woningen en de bewoners in de gebouwen te schatten.
a) Uit de beschikbare informatie blijkt dat de woningen in een flatgebouw zo zijn ingedeeld dat ze een enkele gevel hebben die aan lawaai wordt blootgesteld.
In dit geval wordt de toewijzing van het aantal woningen en bewoners aan waarneempunten gewogen op basis van de lengte van de vertegenwoordigde gevel volgens de procedure van geval 1 of geval 2, zodat de som van alle waarneempunten het totale aantal woningen en bewoners die aan het gebouw zijn toegewezen, vertegenwoordigt.
b) Uit de beschikbare informatie blijkt dat woningen in een flatgebouw zo zijn ingedeeld dat er meer dan een enkele gevel aan lawaai wordt blootgesteld, of dat er geen informatie beschikbaar is over het aantal gevels van de woningen dat aan lawaai wordt blootgesteld.
In dit geval wordt voor elk gebouw de reeks van bijbehorende waarneemlocaties verdeeld in een onderste en bovenste helft op basis van de mediaanwaarde2 van de berekende beoordelingsniveaus voor elk gebouw. In het geval van een oneven aantal waarneempunten wordt de procedure toegepast met uitzondering van de waarneemlocatie met het laagste geluidsniveau.
Voor elk waarneempunt in de bovenste helft van de gegevensreeks wordt het aantal woningen en de bewoners gelijkelijk verdeeld, zodat de som van alle waarneempunten in de bovenste helft van de gegevensreeks het totale aantal woningen en bewoners vertegenwoordigt. Er worden geen woningen of bewoners toegewezen aan de waarneempunten in de onderste helft van de gegevensreeks3.
De Regeling geluid milieubeheer wordt als volgt gewijzigd:
A
Artikel 4 komt te luiden:
Als agglomeratie als bedoeld in artikel 11.5 van de wet worden aangewezen:
a. de agglomeratie Amsterdam/Haarlem, omvattende de gemeenten:
Aalsmeer, Amstelveen, Amsterdam, Beverwijk, Bloemendaal, Diemen, Haarlem, Haarlemmermeer, Heemskerk, Heemstede, Ouder-Amstel, Uithoorn, Velsen, Zaanstad, Zandvoort;
b. de agglomeratie Den Haag/Leiden, omvattende de gemeenten:
Delft, Den Haag, Katwijk, Leiden, Leiderdorp, Leidschendam-Voorburg, Midden-Delfland, Oegstgeest, Pijnacker-Nootdorp, Rijswijk, Voorschoten, Wassenaar, Westland, Zoetermeer;
c. de agglomeratie Eindhoven, omvattende de gemeenten:
Best, Eindhoven, Geldrop-Mierlo, Helmond, Nuenen, Gerwen en Nederwetten, Veldhoven;
d. de agglomeratie Heerlen/Kerkrade, omvattende de gemeenten:
Beekdaelen, Brunssum, Heerlen, Kerkrade, Landgraaf, Voerendaal;
e. de agglomeratie Rotterdam/Dordrecht, omvattende de gemeenten:
Albrandswaard, Barendrecht, Capelle aan den IJssel, Dordrecht, Hendrik-Ido-Ambacht, Maassluis, Nissewaard, Papendrecht, Ridderkerk, Rotterdam, Schiedam, Sliedrecht, Vlaardingen, Zwijndrecht;
f. de agglomeratie Utrecht, omvattende de gemeenten:
Houten, Nieuwegein, Stichtse Vecht, Utrecht, IJsselstein;
g. de agglomeratie Alkmaar, omvattende de gemeenten:
Alkmaar, Bergen, Dijk en Waard, Heiloo;
h. de agglomeratie Enschede, omvattende de gemeenten:
Almelo, Enschede, Hengelo;
i. agglomeratie Gouda, omvattende de gemeenten:
Alphen aan de Rijn, Gouda, Waddinxveen;
j. de agglomeratie Hilversum, omvattende de gemeenten;
Blaricum, Gooise Meren, Hilversum, Huizen, Laren, Weesp;
k. Almere;
l. Amersfoort;
m. Apeldoorn;
n. Arnhem;
o. Breda;
p. ‘s-Hertogenbosch;
q. Groningen;
r. Maastricht;
s. Nijmegen;
t. Tilburg;
u. Zwolle.
B
Na artikel 4 wordt een artikel ingevoegd, luidende:
De geluidsbelasting Lden en de geluidsbelasting Lnight, beiden als gevolg van vliegtuiglawaai, worden bepaald overeenkomstig bijlage II van de Richtlijn 2002/49/EG van het Europees parlement en de Raad van 25 juni 2002 inzake de evaluatie en beheersing van omgevingslawaai (PbEU 2002, L 189).
C
Artikel 9 komt te luiden:
Het aantal bewoners van woningen per geluidsbelastingklasse dat door een of meer geluidsbronnen in hoge mate wordt gehinderd dan wel van wie daardoor de slaap in hoge mate wordt verstoord, en de toename van het aantal gevallen van ischemische hartziekten (IHD) door wegverkeerslawaai, worden bepaald door middel van de desbetreffende in bijlage 2 bij deze regeling opgenomen dosis-effectrelaties.
D
Bijlage 2 komt te luiden:
Voor de bepaling van schadelijke effecten wordt het volgende in aanmerking genomen:
• ischemische hartziekten vallend onder codes BA40 tot en met BA6Z van de internationale classificatie ICD-11 van de Wereldgezondheidsorganisatie (IHD);
• hoge mate van hinder (HA);
• hoge mate van slaapverstoring (HSD).
De schadelijke effecten worden berekend door middel van een van de volgende formules, zoals nader gespecificeerd in paragrafen 2.1 tot en met 2.3:
• het relatieve risico (RR) van het schadelijke effect:
|
|
(1) |
• het absolute risico (AR) van het schadelijke effect:
|
|
(2) |
Voor de berekening van het relatieve risico (RR) wat het schadelijke effect van ischemische hartziekten (IHD) betreft, wordt voor het gebied waarbinnen de incidentie bekend is (i) de volgende dosis/effectrelatie gebruikt:
|
|
(3) |
|
voor wegverkeerslawaai.
De blootstelling van de bevolking wordt voor elke geluidbronsoort en elk schadelijk effect afzonderlijk bepaald. Wanneer dezelfde personen tegelijkertijd aan verschillende geluidbronsoorten worden blootgesteld, mogen de schadelijke effecten – in het algemeen – niet worden gecumuleerd. Die effecten kunnen evenwel met elkaar worden vergeleken, om het relatieve belang van elke geluidbronsoort te kunnen bepalen.
Wat IHD in geval van lawaai van wegverkeer betreft, wordt het aandeel van de gevallen van specifieke schadelijke effecten in de bevolking die wordt blootgesteld aan een RR dat volgens de berekening wordt veroorzaakt door omgevingslawaai, voor het gebied waarbinnen de incidentie bekend is (i) afgeleid door:
|
|
(10) |
waarbij
• PAFIHD,road de aan de bevolking toe te schrijven fractie is;
• de reeks j blootstellingsbereiken bestaat uit afzonderlijke bereiken van maximaal 5 dB
• pj het aandeel van de totale bevolking P is in het beoordeelde gebied dat wordt blootgesteld aan blootstellingsbereik j, dat wordt geassocieerd met een bepaald RR van het schadelijk effect IHDroad
• RRj,IHD,road wordt berekend met formule 3, bij de centrale waarde van elk blootstellingsbereik.
Wat IHD in geval van lawaai van wegverkeer betreft, is het totale aantal N gevallen per gebied waarbinnen de incidentie bekend is (i):
|
|
(11) |
waarbij
• PAFIHD,road,i wordt berekend met formule 8;
• IIHD,i de incidentie van IHD is in het te beoordelen gebied i, die kan worden verkregen uit statistieken over de gezondheid van de desbetreffende regio of het desbetreffende land;
• Pi de totale bevolking is van het te beoordelen gebied i.
Wat hoge mate van hinder (HA) en hoge mate van slaapverstoring (HSD) in geval van lawaai van wegverkeer, treinverkeer en vliegtuigen betreft, is het totale aantal N personen die schadelijk effect x ondergaan (aantal toe te schrijven gevallen) vanwege geluidbronsoort y:
|
|
(12) |
waarbij
• ARj,x,y het absolute risico (AR) is van het desbetreffende schadelijke effect x (HA, HSD), dat wordt berekend met de in paragrafen 2.2 en 2.3 van deze bijlage beschreven formules, bij de centrale waarde van elk blootstellingsbereik;
• nj het aantal personen is dat wordt blootgesteld aan het blootstellingsbereik j.
De Regeling omgevingslawaai luchtvaart wordt als volgt gewijzigd:
A
Artikel 2 komt te luiden:
1. De geluidbelasting Lden en de geluidbelasting Lnight worden bepaald overeenkomstig bijlage II van de Richtlijn 2002/49/EG van het Europees parlement en de Raad van 25 juni 2002 inzake de evaluatie en beheersing van omgevingslawaai (PbEU 2002, L 189).
2. De gezondheidseffecten van luchtvaartlawaai worden bepaald overeenkomstig de methode opgenomen in bijlage Bepalingsmethode gezondheidseffecten bij deze regeling.
B
Artikel 4, tweede lid, komt te luiden:
2. Voor de toepassing van het eerste lid, onder b, wordt het aantal bewoners van woningen bepaald overeenkomstig de gemiddelde huishoudensgrootte volgens de meest recente publicatie van het Centraal Bureau voor de Statistiek.
C
Aan de regeling wordt een bijlage toegevoegd, luidende:
Voor de berekening van het absolute risico op hoge mate van hinder ARHA door vliegtuiglawaai wordt de volgende dosis-effectrelatie gebruikt:
|
|
(1) |
Voor de berekening van het absolute risico op hoge mate van slaapverstoring ARHSD door vliegtuiglawaai wordt de volgende dosis-effectrelatie gebruikt:
|
|
(2) |
Deze regeling zal met de toelichting in de Staatscourant worden geplaatst.
De Minister van Infrastructuur en Waterstaat, M.G.J. Harbers
De Staatssecretaris van Infrastructuur en Waterstaat, V.L.W.A. Heijnen
Met deze regeling worden wijzigingen doorgevoerd in het Reken- en meetvoorschrift geluid 2012, de Regeling geluid milieubeheer en de Regeling omgevingslawaai luchtvaart.
Hiermee wordt de wijziging van bijlage II en bijlage III bij Richtlijn 2002/49/EG van het Europees parlement en de Raad van 25 juni 2002 inzake de evaluatie en de beheersing van omgevingslawaai (PbEU 2002, L 189) (hierna: richtlijn omgevingslawaai) geïmplementeerd.
Daarnaast wordt het moment van deze wijziging aangegrepen om een technische wijziging aan te brengen, te weten de actualisatie van de aanwijzing van agglomeraties.
Voor de kartering van geluid wordt een uniforme rekenmethode toegepast conform de richtlijn omgevingslawaai. Deze rekenmethode wordt ook wel Cnossos genoemd. Op 21 december 2020 heeft de Europese Commissie bijlage II bij de richtlijn omgevingslawaai gewijzigd.4 Het betreft wijzigingen van de gemeenschappelijke bepalingsmethoden voor lawaai met het oog op de wetenschappelijke en technische vooruitgang. Met de wijziging van bijlage VII van het Reken- en meetvoorschrift geluid 2012 worden deze aanpassingen geïmplementeerd.
Op verschillende punten wordt afgeweken van de door de Europese Commissie voorgeschreven wijzigingen. Dit betreft:
• Wijzigingen in verband met tekstconformiteit vanwege kennelijke fouten in de Nederlandse vertaling van de wijzigingsrichtlijn, waarbij de Nederlandse vertaling inhoudelijk afwijkt van de Engelstalige versie en andere taalversies.
• Harmonisatie van wiskundige notaties en terminologie met het Reken- en meetvoorschrift geluid 2012. Deze harmonisatie heeft geen inhoudelijke gevolgen. Een voorbeeld hiervan is het gebruik van een punt als decimaalteken in de wijzigingsrichtlijn van de Europese Commissie en het gebruik van komma als decimaalteken in het Reken- en meetvoorschrift geluid 2012.
• Wijzigingen die betrekking hebben op luchtvaartlawaai zijn niet opgenomen, omdat de bepalingsmethode voor luchtvaartlawaai niet onder het Reken- en meetvoorschrift geluid 2012 valt.
• Herstel van een fout in de bestaande notatie van formule 2.5.12 voor geometrische divergentie.
Bij de implementatie van de uniforme rekenmethode hebben lidstaten een aantal keuzemogelijkheden, waaronder de keuze voor het vaststellen van nationale emissiekentallen. Nederland heeft gebruikgemaakt van deze keuzemogelijkheden door eigen emissiekentallen vast te stellen. Zo is met de wijziging van bijlage IV bij het Reken- en meetvoorschrift geluid 2012 (Stcrt. 2021, 10294) reeds als aanvulling op de al vastgestelde emissiekentallen een nieuwe spoorvoertuigcategorie 12 toegevoegd en zijn voertuigtypes ICM III en ICR in spoorvoertuigcategorie 8 geplaatst.
De wijziging van bijlage II van de richtlijn omgevingslawaai betrof voor railverkeer onder andere een bijgestelde set contactfilters, die het contact van de wielen met de spoorstaaf beschrijven, en de introductie van een nieuwe aanpak voor de geluidemissie van spoorbruggen. Deze wijzigingen vergen een aanpassing van de parameterwaarden die voor het Nederlandse spoor zijn vastgesteld. De aangepaste parameterwaarden zijn gebaseerd op de onderzoeksnotitie ‘dBvision (2021), Actualisatie spoorparameters CNOSSOS-NL’.
Met deze wijziging van bijlage VII worden wegdekcorrectiefactoren van twee wegdektypen opgenomen. De vaststelling van nationale emissiekentallen voor wegverkeer ging gepaard met wegdekcorrectiefactoren voor een aantal (standaard) wegdektypen. Sindsdien zijn er diverse nieuwe wegdektypen ontwikkeld waarop specifieke wegdekcorrectiefactoren van toepassing zijn, aanvullend op de al bestaande wegdektypen. Op basis van onderzoek van het RIVM zijn met deze wijziging twee nieuwe typen wegdek aan het Reken- en meetvoorschrift geluid 2012 toegevoegd, te weten: Akoestisch geoptimaliseerd enkellaags zeer open asfaltbeton (1L ZOAB) en Akoestisch geoptimaliseerd steenmastiekasfalt (SMA).
De verplichting voor agglomeraties om geluidsbelastingkaarten op te stellen was in eerste instantie beperkt tot agglomeraties met 250.000 inwoners en meer. Vanaf de tweede tranche van de geluidkartering, in 2012, gold die verplichting ook voor agglomeraties met 100.000 inwoners en meer. Sinds die uitbreiding van de lijst van aangewezen gemeentes zijn er verscheidene gemeentelijke herindelingen geweest. Met de wijziging van artikel 4 van de Regeling geluid milieubeheer (hierna: Rgm) worden de aangewezen gemeentes weer in lijn gebracht met de bestaande gemeentelijke indeling. De wijzigingen hebben betrekking op de agglomeraties Amsterdam/Haarlem, Den Haag/Leiden, Heerlen/Kerkrade, Rotterdam/Dordrecht, Utrecht, Alkmaar, Gouda en Hilversum. In sommige gevallen leidt dit tot een groter gebied waarvoor de kartering moet worden uitgevoerd, bijvoorbeeld bij een fusie van twee gemeenten waarvan er één geen deel uitmaakte van de oorspronkelijke agglomeratie.
In bijlage IV bij de richtlijn omgevingslawaai is aangegeven dat bij strategische geluidsbelastingkaarten voor agglomeraties speciaal aandacht moet worden besteed aan wegverkeer, spoorverkeer, luchthavens en industrieterreinen, waaronder havens, als deze van invloed zijn op de geluidsbelasting in de agglomeratie. In artikel 4a van de Rgm is de voor luchtvaartlawaai te gebruiken rekenmethode aangewezen. Voor wegverkeer, spoorverkeer en industrieterreinen is de rekenmethode opgenomen in het Reken- en meetvoorschrift geluid 2012.
De herziening van bijlage 2 van de Rgm vindt plaats ter implementatie van Richtlijn (EU) 2020/367 van de Commissie van 4 maart 2020 tot wijziging van bijlage III bij Richtlijn 2002/49/EG van het Europees parlement en de Raad wat de vaststelling van bepalingsmethoden voor de schadelijke effecten van omgevingslawaai betreft (PbEU 2020, L 67). Deze richtlijn is gebaseerd op onderzoek dat is uitgevoerd en gepubliceerd door de Wereldgezondheidsorganisatie (hierna: WHO).5 Voor een toelichting wordt verwezen naar het artikelsgewijze deel van de toelichting.
De Regeling omgevingslawaai luchtvaart maakt onderdeel uit van de uitvoering van de richtlijn omgevingslawaai. Deze richtlijn is voor de belangrijke luchthavens geïmplementeerd in hoofdstuk 8 van de Wet luchtvaart. In de praktijk is deze regeling alleen op de luchthaven Schiphol van toepassing, omdat dit de enige Nederlandse luchthaven is die voldoet aan de definitie van belangrijke luchthavens in de richtlijn omgevingslawaai.
Bij de invoering van de Regeling omgevingslawaai luchtvaart waren de bepalingsmethoden voor gezondheidseffecten nog niet in de richtlijn omgevingslawaai vastgelegd. Inmiddels zijn deze bepalingsmethoden wel in de richtlijn omgevingslawaai opgenomen. Door toevoeging van een tweede lid aan artikel 2 worden deze bepalingsmethoden in de Regeling omgevingslawaai luchtvaart geïmplementeerd.
In artikel 4, tweede lid, is vastgelegd hoe het aantal inwoners per geluidbelastingklasse moet worden bepaald aan de hand van het aantal woningen per geluidbelastingklasse. Met de wijziging van dit artikellid is ervoor gezorgd dat dit gebeurt op basis van de meest actuele, landelijk beschikbare gegevens. Met deze wijziging wordt de tekst in overeenstemming gebracht met de bepaling in artikel 6 van de Regeling geluid milieubeheer, die van toepassing is op wegverkeerslawaai, spoorweglawaai en industrielawaai.
De regeling zorgt voor eenduidigheid over de te hanteren rekenmethode voor de geluidsbelastingkaarten en voor het bepalen van gezondheidseffecten voor de bevolking. Daarnaast is duidelijk welke gemeentes een geluidsbelastingkaart en een geluidactieplan moeten opstellen ter uitvoering van de richtlijn omgevingslawaai.
De regeling heeft geen gevolgen voor de bestuurlijke lasten van gemeenten en provincies en heeft naar haar aard ook geen gevolgen voor de administratieve lasten van burgers.
Van internetconsultatie is afgezien, omdat de regeling in de artikelen I, II, onderdeel B tot en met D, en III implementatie betreft van de wijziging van de bijlagen II en III van de richtlijn omgevingslawaai en de wijziging in artikel II, onderdeel A, de actualisatie betreft van agglomeraties.
Met dit artikel wordt bijlage VII bij het Reken- en meetvoorschrift geluid 2012 gewijzigd. Hiermee wordt de richtlijn geïmplementeerd van de Europese Commissie van 21 december 2020 tot wijziging van bijlage II bij Richtlijn 2002/49/EG van het Europees parlement en de Raad betreffende de gemeenschappelijke bepalingsmethoden voor lawaai met het oog op aanpassing aan de wetenschappelijke en technische vooruitgang (PbEU 2021, L 269). Voor de toelichting wordt verwezen naar het algemene deel van de toelichting.
De wijzigingen betreffen wijzigingen in notaties van formules en tabellen. Vanwege het grote aantal wijzigingen in notaties van formules en tabellen is gekozen voor het geheel opnieuw vaststellen van hoofdstuk 2 van bijlage VII. De specifieke punten waarop de rekenmethode is aangepast, zijn aangegeven in de wijzigingsrichtlijn6 en beschreven in de rapportage die het RIVM hierover heeft opgesteld7.
Tegelijkertijd met de wijzigingen die voortvloeien uit de wijzigingsrichtlijn is de methode gewijzigd om de richtingsafhankelijke optreedfrequentie p van gunstige omstandigheden te bepalen voor ieder afzonderlijk voortplantingspad van een geluidbron naar een waarneempunt. Tabel 2.5.a, waarin de optreedfrequentie in stappen van 20 graden gegeven was, is daarbij vervangen door de nieuwe formule 2.5.9b. Hierdoor kent de richtingsafhankelijke optreedfrequentie p geen discrete overgangen meer en is er sprake van een volledig continu verloop.
Het moment van de wijziging van de Rgm is aangegrepen om de op grond van artikel 11.5 van de Wet milieubeheer aangewezen agglomeraties te actualiseren.
Het gaat om de volgende wijzigingen:
• Agglomeratie Alkmaar:
○ Verwijderen gemeenten Heerhugowaard en Langedijk (per 1 januari 2022 gefuseerd tot de nieuwe gemeente Dijk en Waard);
○ Toevoegen gemeente Dijk en Waard;
• Agglomeratie Amsterdam/Haarlem:
○ Verwijderen gemeente Bennebroek (per 1 januari 2009 gefuseerd met de gemeente Bloemendaal);
○ Verwijderen gemeente Haarlemmerliede en Spaarnwoude (per 1 januari 2019 gefuseerd met de gemeente Haarlemmermeer);
• Agglomeratie Den Haag/Leiden:
○ Verwijderen gemeenten Rijnsburg en Valkenburg (per 1 januari 2006 gefuseerd met de gemeente Katwijk);
• Agglomeratie Rotterdam/Dordrecht:
○ Verwijderen gemeente Rozenburg (per 1 januari 2010 gefuseerd met de gemeente Rotterdam)
○ Verwijderen gemeente Spijkenisse (per 1 januari 2015 gefuseerd met de gemeente Bernisse tot de nieuwe gemeente Nissewaard);
○ Toevoegen gemeente Nissewaard;
• Agglomeratie Utrecht:
○ Verwijderen gemeente Maarssen (per 1 januari 2011 gefuseerd met de gemeenten Breukelen en Loenen tot de nieuwe gemeente Stichtse Vecht)
○ Toevoegen gemeente Stichtse Vecht;
• Agglomeratie Gouda:
○ Verwijderen gemeente Boskoop (per 1 januari 2014 gefuseerd met de gemeenten Alphen aan den Rijn en Rijnwoude tot fusiegemeente Alphen aan den Rijn);
• Agglomeratie Hilversum:
○ Verwijderen gemeenten Bussum en Naarden (per 1 januari 2016 gefuseerd met de gemeente Muiden tot de nieuwe gemeente Gooise Meren);
○ Toevoegen gemeente Gooise Meren;
De richtlijn omgevingslawaai schrijft voor dat de waarden van Lden en Lnight moeten worden bepaald volgens de in bijlage II van de richtlijn opgenomen methode. Dit is nagenoeg een kopie van ECAC Doc29, vierde editie. Doc29 beschrijft een voor Europa geharmoniseerde methode om de geluidsbelasting rondom civiele luchthavens te bepalen. In het toepassingsgebied van Doc29 staat dat de jaargemiddelde geluidsbelasting in Lden en Lnight alleen kan worden bepaald voor luchthavenluchtverkeer dat grotendeels bestaat uit zware vliegtuigen (handelsverkeer). Het bepalen van Lden en Lnight van luchthavenluchtverkeer dat grotendeels bestaat uit militaire vliegtuigen, lichte vliegtuigen en helikopters valt niet binnen het toepassingsgebied van Doc29. In bijlage II is het toepassingsgebied uitgebreid met lichte vliegtuigen en helikopters. Er zijn brongegevens van een beperkt aantal typen lichte vliegtuigen en helikopers opgenomen in bijlage II.
In bijlage IV bij de richtlijn omgevingslawaai staat dat bij het opstellen van strategische geluidsbelastingkaarten voor agglomeraties aandacht moet worden besteed aan lawaai van luchthavens. De richtlijn schrijft voor dat de waarden van Lden en Lnight moeten worden bepaald volgens de in bijlage II van de richtlijn opgenomen methode. Het toepassingsgebied van bijlage II omvat onder andere lichte vliegtuigen en helikopters. Echter geluidemissiegegevens van slechts een beperkt aantal typen lichte vliegtuigen en helikopers zijn opgenomen in bijlage II. Als het luchthavenluchtverkeer grotendeels bestaat uit lichte vliegtuigen of helikopters, kan, vanwege het ontbreken van voldoende representatieve geluidemissiegegevens en bij toewijzing aan de vliegtuigtypen die wel in de rekenmethode beschikbaar zijn, een onder- of overschatting van de geluidsbelasting ontstaan, met doorwerking in de geluidcontouren.
De richtlijn omgevingslawaai geeft aan dat lawaai veroorzakende activiteiten (zoals helikopters, taxiën, proefdraaien en het gebruik van hulpaggregaten) die niet wezenlijk bijdragen aan de totale blootstelling van de bevolking aan vliegtuiglawaai en de bijbehorende geluidscontouren, kunnen worden uitgesloten. Aangezien voor luchthavens met overwegend lichte vliegtuigen of helikopters niet altijd voldoende vast staat of de rekenuitkomsten representatief zijn, kan een andere rekenmethode worden gebruikt om een oordeel te vellen of de bijdrage wezenlijk is. Daarnaast geldt dat voor proefdraaien en het gebruik van hulpaggregaten een andere rekenmethode dan die voor vliegtuiglawaai uit bijlage II moet worden gebruikt. Ook de mate waarin er overschrijding van de wettelijke grenswaarden (voor regionale luchthavens is dat 56 dB Lden bepaald met de daarvoor van toepassing zijnde rekenmethode) in een agglomeratie optreedt, is van belang bij de afweging of het vliegtuiglawaai voor een agglomeratie relevant is. Het is aan het bevoegd gezag om te bepalen of luchthavenluchtverkeer kan worden uitgesloten of moet worden meegenomen bij het opstellen van geluidkaarten en geluidactieplannen.
De regeling wijzigt artikel 9 van de Regeling geluid milieubeheer. Voor de toelichting wordt verwezen naar onderdeel D van deze toelichting.
Bijlage 2 bij de Rgm is geheel herzien. In deze bijlage zijn voor geluidactieplannen die moeten worden opgesteld in het kader van de richtlijn omgevingslawaai de dosis-effectrelaties vastgelegd tussen de hoeveelheid geluid en de statistische kans op gezondheidseffecten bij mensen die daar aan worden blootgesteld.
Met de herziening wordt invulling gegeven aan de richtlijn van de Europese Commissie van 4 maart 2020 tot wijziging van bijlage III bij Richtlijn 2002/49/EG van het Europees parlement en de Raad wat de vaststelling van bepalingsmethoden voor de schadelijke effecten van omgevingslawaai betreft (PbEU 2020, L 67).
De bestaande dosis-effectrelaties, waarmee het aantal gehinderden en ernstig gehinderden op basis van de dosismaat Lden en het aantal slaapgestoorden op basis van de dosismaat Lnight waren beschreven voor industrielawaai, wegverkeerslawaai en spoorweglawaai, zijn komen te vervallen. Hiervoor in de plaats zijn dosis-effectrelaties gekomen die voor wegverkeerslawaai, spoorweglawaai en vliegtuiglawaai de hoge mate van hinder op basis van de dosismaat Lden en de hoge mate van slaapverstoring op basis van de dosismaat Lnight beschrijft. Tevens worden dosis-effectrelaties voor het relatieve risico op ischemische hartziekten (IHD) door wegverkeerslawaai gegeven, op basis van de dosismaat Lden. Voor andere geluidbronsoorten heeft de WHO die relatie niet met voldoende zekerheid kunnen vaststellen en is er om die reden geen dosis-effectrelatie met betrekking tot IHD opgenomen in de richtlijn omgevingslawaai.
In figuur 1 zijn voor wegverkeerslawaai de bestaande en
nieuwe dosis-effectrelatie voor hoge mate van hinder grafisch weergegeven. In
deze figuur is halverwege elk blootstellingsbereik van 5 dB een markering
aangebracht, maar de nieuwe dosis-effectrelatie kan ook worden gebruikt voor
een smaller blootstellingsbereik, bijvoorbeeld van 1 dB. De bestaande en nieuwe
dosis-effectrelatie voor hoge mate van hinder door spoorweglawaai zijn in
figuur 2 weergegeven. De waarden in het midden van het 5 dB
blootstellingsbereik zijn opgenomen in tabel A, voor zowel wegverkeerslawaai
als spoorweglawaai.
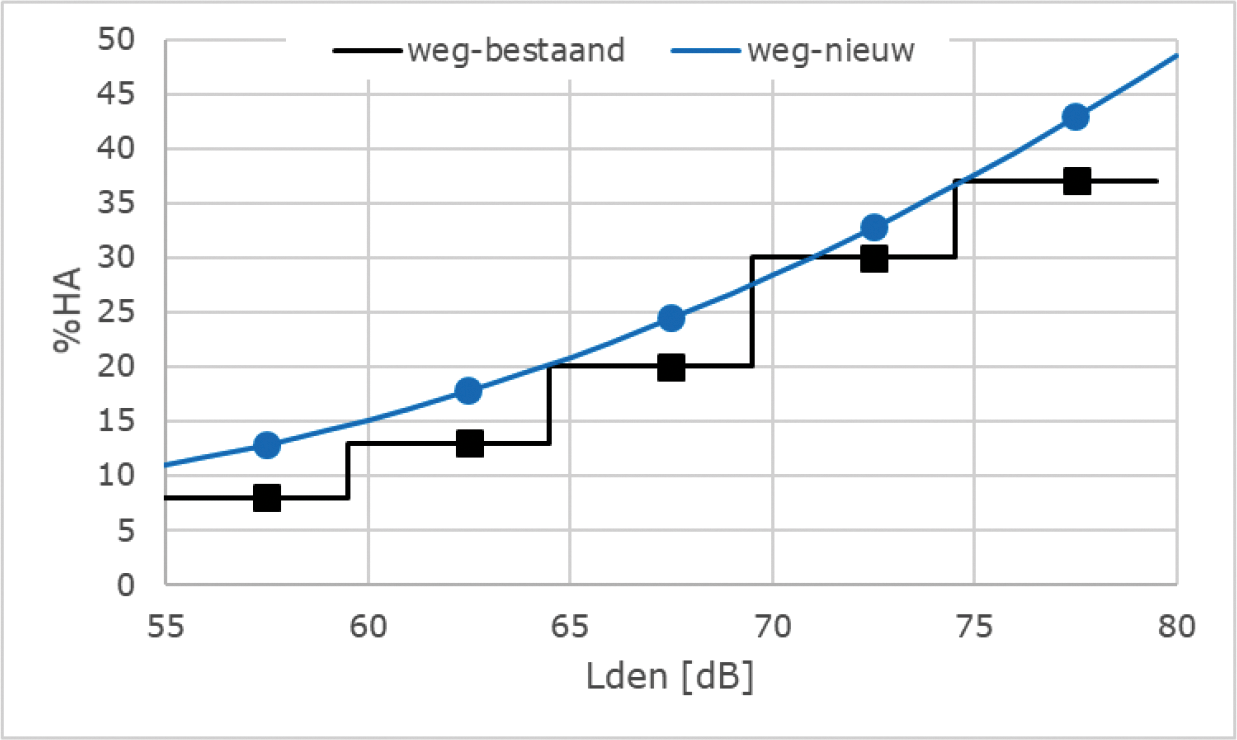
Figuur 1
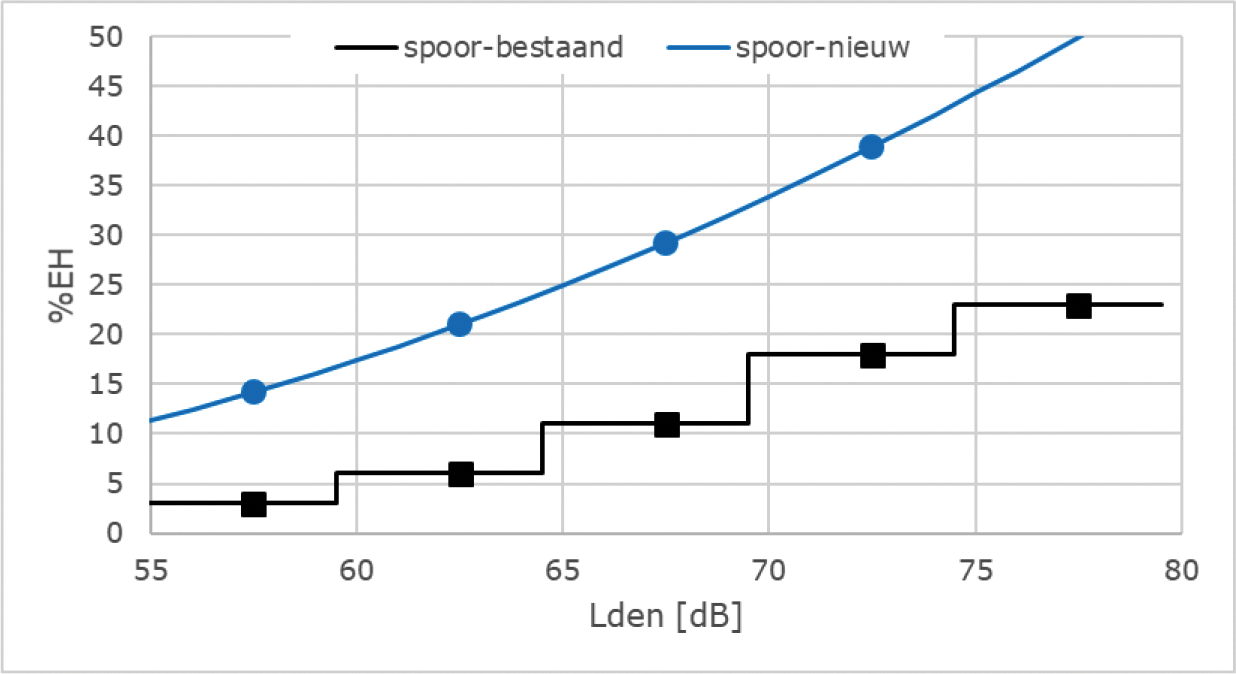
Figuur 2
|
Wegverkeerslawaai |
Spoorweglawaai |
|||
|---|---|---|---|---|
|
Blootstellingsbereik (Lden) |
Bestaand |
Nieuw |
Bestaand |
Nieuw |
|
55-59 dB |
8% |
13% |
3% |
14% |
|
60-64 dB |
13% |
18% |
6% |
21% |
|
65-69 dB |
20% |
24% |
11% |
29% |
|
70-74 dB |
30% |
33% |
18% |
39% |
|
75-79 dB |
37% |
43% |
23% |
50% |
Momenteel is slechts geringe kennis beschikbaar over de schadelijke effecten van industrielawaai en het is derhalve niet mogelijk om een gemeenschappelijke methode voor de bepaling ervan te ontwikkelen. De Europese Commissie heeft in de richtlijn aangegeven daar via toekomstige herzieningen in te willen voorzien. Bij het beschrijven van de ontwikkeling van de gezondheidseffecten door industrielawaai in het kader van geluidactieplannen kan gebruik worden gemaakt van de dosis-effectrelaties die golden voor inwerkingtreding van deze regeling.
Het gebruik van de herziene dosis-effectrelaties is verplicht vanaf de eerstvolgende EU geluidactieplannen, die in 2024 moeten worden vastgesteld.
De richtlijn omgevingslawaai staat toe dat andere dosis-effectrelaties worden gebruikt dan die uit de richtlijn, mits zij zijn gebaseerd op kwalitatief hoogwaardige en statistisch significante studies. De WHO heeft in zijn richtlijnen aangegeven dat dosis-effectrelaties die in een lokale context zijn vastgesteld, de voorkeur verdienen boven de generieke dosis-effectrelaties die in bijlage III van de richtlijn omgevingslawaai zijn opgenomen voor de Europese regio als geheel.
Voor Schiphol is een dergelijke studie beschikbaar, de Gezondheidskundige Evaluatie Schiphol (GES) uit 2002. Voor andere Nederlandse luchthavens zijn geen specifieke dosis-effectrelaties beschikbaar. Ook voor deze luchthavens worden de dosis-effectrelaties van Schiphol, die meer specifiek op de Nederlandse situatie van toepassing zijn dan de in de richtlijn opgenomen generieke relaties, geschikter geacht dan die uit bijlage III van de richtlijn omgevingslawaai.
In het aanvullingsspoor geluid Omgevingswet zijn de inzichten uit het WHO-onderzoek en een daarover nog te bepalen kabinetsstandpunt niet verwerkt, om de inwerkingtreding van de Omgevingswet niet te beïnvloeden en ten behoeve van de beleidsneutrale implementatie van de doelen en uitgangspunten van het beleidsvernieuwingstraject SWUNG-2. Om dezelfde reden is er nu voor gekozen om de rekenmethode voor de cumulatieve geluidsbelasting, in bijlage 1 van het Reken- en meetvoorschrift geluid 2012, niet te wijzigen, ofschoon die rekening houdt met de verschillen in dosis-effectrelaties van de verschillende geluidsbronnen. Eventuele wijzigingen in die rekenmethode zullen na inwerkingtreding van de Omgevingswet worden doorgevoerd in samenhang met de eventuele andere beleidswijzigingen die voortvloeien uit de WHO-richtlijnen.
De regeling wijzigt artikel 2 en artikel 4, tweede lid, van de Regeling omgevingslawaai luchtvaart. Voor de toelichting wordt verwezen naar het algemene deel van de toelichting.
De dosis-effectrelaties zijn gebaseerd op de gegevens verkregen met de Gezondheidskundige Evaluatie Schiphol (GES) uit 2002 en gecorrigeerd voor het gebruik van geluidbelastingen verkregen met ECAC Doc29, vierde editie.8 Daarmee zijn ze meer specifiek voor de Nederlandse situatie dan de in de richtlijn opgenomen generieke relaties. De relaties zijn noodzakelijk voor het in beeld kunnen brengen van gezondheidseffecten rondom belangrijke luchthavens (en in agglomeraties).
De datum van inwerkingtreding van de artikelen I, II, onderdelen B, C en D, en III van deze regeling volgt uit artikel 2, eerste lid, van Richtlijn (EU) 2020/367 van 4 maart 2020 tot wijziging van bijlage III bij Richtlijn 2002/49/EG van het Europees Parlement en de Raad wat de vaststelling van bepalingsmethoden voor de schadelijke effecten van omgevingslawaai betreft (PbEU 2020, L67) en uit artikel 2, eerste lid, van Richtlijn (EU) 2021/1226 van 21 december 2020 tot wijziging van bijlage II bij Richtlijn 2002/49/EG van het Europees Parlement en de Raad betreffende de gemeenschappelijke bepalingsmethoden voor lawaai met het oog op aanpassing aan de wetenschappelijke en technische vooruitgang (PbEU 2021, L 269). In deze artikelen is voorgeschreven dat uiterlijk op 31 december 2021 aan de richtlijnen moeten zijn voldaan.
Vanwege raakvlakken tussen de wijziging van bijlage III bij de richtlijn omgevingslawaai met het lopende interbestuurlijke traject met de Bestuurlijke Regie Schiphol, de VNG en het IPO rond cumulatie van luchtvaartlawaai in samenhang met de woningbouwopgave voor gemeentes rond luchthaven Schiphol heeft hierover nader bestuurlijk contact plaatsgevonden alvorens de implementatie in de Regeling geluid milieubeheer en in de Regeling omgevingslawaai luchtvaart af te ronden. Dit heeft geleid tot beperkte vertraging in het implementatietraject, waardoor dit traject nog niet was afgerond op 31 december 2021. Om die reden is terugwerkende kracht verleend aan artikel I, artikel II, onderdeel B, C en D en artikel III van deze regeling die de implementatie betreffen van genoemde richtlijnen. Tijdige implementatie van de gewijzigde richtlijnen is van belang voor de instanties die verantwoordelijk zijn voor het opstellen van strategische geluidbelastingkaarten. Daarbij gaat het om de implementatie van gewijzigde rekenregels in software, het uitvoeren van berekeningen en het vaststellen en publiceren van de kaarten. Uiterlijk 30 juni 2022 moeten de geluidbelastingkaarten zijn vastgesteld.
De Minister van Infrastructuur en Waterstaat, M.G.J. Harbers
De Staatssecretaris van Infrastructuur en Waterstaat, V.L.W.A. Heijnen
|
Richtlijn (EU) 2021/1226 |
Bepaling in implementatieregeling of bestaande regeling: |
Omschrijving beleidsruimte |
Toelichting op de keuze(n) bij de invulling van de beleidsruimte |
|---|---|---|---|
|
Artikel 1 (wijzigingen in tekst bijlage II)1: |
Hoofdstuk 2 van bijlage VII bij het Reken- en meetvoorschrift geluid 2012: |
||
|
1) punt 2.1.1 |
punt 2.1.1 |
Geen |
– |
|
2) punt 2.2.1 |
punt 2.2.1 |
Geen |
– |
|
3) tabel 2.3.b |
tabel 2.3.b1 |
Geen |
– |
|
4) punt 2.3.2 |
punt 2.3.2 |
Geen |
– |
|
5) punt 2.3.3 |
punt 2.3.3 |
Geen |
– |
|
6) punt 2.4.1 |
punt 2.4.1 |
Geen |
– |
|
7) punt 2.5.1 |
punt 2.5.1 |
Geen |
– |
|
8) punt 2.5.5 |
punt 2.5.5 |
Geen |
– |
|
9) punt 2.5.6 |
punt 2.5.6 |
Geen |
– |
|
17) punt 2.8 |
punt 2.6 |
Geen |
– |
|
19) a: tabel F-1, b: tabel F-4 |
a: tabel 2.2b, b: tabel 2.2.d |
Mogelijkheid om waardes aan te passen |
De waardes in de tabellen zijn aangepast aan het Nederlandse wagenpark en de in Nederland beschikbare wegdekproducten |
|
20) a: tabel G-1, b: tabel G-2, c: tabel G-3, d: tabel G-3, e: tabel G-4, f: tabel G-5, g: tabel G-6, h: tabel G-7 |
a: tabel 2.3.h, b: tabel 2.3.h, c: tabel 2.3.d, d: tabel 2.3.k, e: tabel 2.3.h, f: tabel 2.3.l, g: tabel 2.3.n, h: tabel 2.3.i2 |
Geen ten aanzien van de inhoud van de tabellen. |
De tabellen hebben ten opzichte van de richtlijn een andere vormgeving vanwege de vertaling van elementaire voertuig en spoorelementen naar de in Nederland gangbare trein- en railtypen |
|
Artikel 2 (implementatiedatum) |
Behoeft naar zijn aard geen implementatie |
Geen |
– |
|
Artikel 3 (inwerkingtreding) |
Behoeft naar zijn aard geen implementatie |
Geen |
– |
|
Artikel 4 (richtlijn gericht tot lidstaten) |
Behoeft naar zijn aard geen implementatie |
Geen |
– |
De wijzigingen in bijlage II ten aanzien van vliegtuiglawaai (wijzigingen 10-16, 18 en 21) worden separaat geïmplementeerd.
|
Richtlijn (EU) 2020/367 |
Bepaling in implementatie-regeling of bestaande regeling: |
Omschrijving beleidsruimte |
Toelichting op de keuze(n) bij de invulling van de beleidsruimte |
|---|---|---|---|
|
Artikel 1 (vervanging gehele tekst bijlage III) |
– Bijlage 2 bij artikel 9 van de Regeling geluid milieubeheer – Bijlage bepalingsmethode gezondheidseffecten, behorend bij artikel 2 van de Regeling omgevingslawaai luchtvaart |
Mogelijkheid om alternatieve lokale dosis-effectrelatie voor luchtvaartlawaai vast te stellen (overweging (3)) |
De richtlijn geeft aan dat alternatieve dosis/effectrelaties die onder plaatselijke omstandigheden zijn vastgesteld, kunnen worden gebruikt, mits zij zijn gebaseerd op kwalitatief hoogwaardige en statistisch significante studies. Van deze mogelijkheid is voor luchtvaartlawaai gebruik gemaakt. |
|
Artikel 2 (implementatie-datum) |
Behoeft naar zijn aard geen implementatie |
Geen |
– |
|
Artikel 3 (inwerking-treding) |
Behoeft naar zijn aard geen implementatie |
Geen |
– |
|
Artikel 4 (richtlijn gericht tot lidstaten) |
Behoeft naar zijn aard geen implementatie |
Geen |
– |
De mediaanwaarde is de waarde die de bovenste helft (50%) van een gegevensreeks scheidt van de onderste helft (50%).
De onderste helft van de gegevensreeks kan worden gelijkgesteld met de aanwezigheid van relatief rustige gevels. Indien vooraf bekend is, bijvoorbeeld op basis van de locatie van gebouwen ten opzichte van de dominante geluidsbronnen, welke meetpuntlocaties plaats zullen maken voor de hoogste/laagste geluidsniveaus, is het niet nodig om het geluid voor de onderste helft te berekenen.
Richtlijn (EU) 2021/1226 van de Commissie van 21 december 2020 tot wijziging van bijlage II bij Richtlijn 2002/49/EG van het Europees parlement en de Raad betreffende de gemeenschappelijke bepalingsmethoden voor lawaai met het oog op aanpassing aan de wetenschappelijke en technische vooruitgang (PbEU 2021, L 269).
Environmental Noise Guidelines for the European Region, Wereldgezondheidsorganisatie 2018, ISBN 978 92 890 5356 3.
Richtlijn (EU) 2021/1226 van de Commissie van 21 december 2020 tot wijziging van bijlage II bij Richtlijn 2002/49/EG van het Europees parlement en de Raad betreffende de gemeenschappelijke bepalingsmethoden voor lawaai met het oog op aanpassing aan de wetenschappelijke en technische vooruitgang (PbEU 2021, L 269).
Amendments for CNOSSOS-EU: Description of issues and proposed solutions, Rijksinstituut voor Volksgezondheid en Milieu RIVM 2019-0023
Kopieer de link naar uw clipboard
https://zoek.officielebekendmakingen.nl/stcrt-2022-103.html
De hier aangeboden pdf-bestanden van het Staatsblad, Staatscourant, Tractatenblad, provinciaal blad, gemeenteblad, waterschapsblad en blad gemeenschappelijke regeling vormen de formele bekendmakingen in de zin van de Bekendmakingswet en de Rijkswet goedkeuring en bekendmaking verdragen voor zover ze na 1 juli 2009 zijn uitgegeven. Voor pdf-publicaties van vóór deze datum geldt dat alleen de in papieren vorm uitgegeven bladen formele status hebben; de hier aangeboden elektronische versies daarvan worden bij wijze van service aangeboden.
