Staatscourant van het Koninkrijk der Nederlanden
| Datum publicatie | Organisatie | Jaargang en nummer | Rubriek | Datum ondertekening |
|---|---|---|---|---|
| Ministerie van Onderwijs, Cultuur en Wetenschap | Staatscourant 2017, 31868 | Besluiten van algemene strekking |
Zoals vergunningen, bouwplannen en lokale regelgeving.
Adressen en contactpersonen van overheidsorganisaties.
U bent hier:

| Datum publicatie | Organisatie | Jaargang en nummer | Rubriek | Datum ondertekening |
|---|---|---|---|---|
| Ministerie van Onderwijs, Cultuur en Wetenschap | Staatscourant 2017, 31868 | Besluiten van algemene strekking |
Het College voor Toetsen en Examens,
Gelet op artikel 3 van de Wet College voor toetsen en examens en artikel 6, eerste lid, onderdeel g, van het Examen- en kwalificatiebesluit beroepsopleidingen WEB.
Gezien de goedkeuring van de Minister van Onderwijs, Cultuur en Wetenschap, gegeven op 17 mei 2017, kenmerk 1183430;
Besluit:
De Regeling omzetting scores in cijfers bij centrale examinering mbo (2015) wordt als volgt gewijzigd:
A
Artikel 1 wordt als volgt gewijzigd:
1. Na ‘geschiedt’ wordt de volgende zinsnede ingevoegd: ‘voor de centrale examens Nederlandse taal en rekenen’.
2. Het begrip ‘bijlage’ wordt vervangen door: bijlage 1.
3. Voor de bestaande tekst wordt het cijfer ‘1.’geplaatst.
4. Er wordt een nieuw lid toegevoegd, luidende:
2. De omzetting van scores in cijfers, bedoeld in artikel 6, eerste lid, onderdeel g, van het Examen- en kwalificatiebesluit beroepsopleidingen WEB geschiedt voor de centrale examens Engels B1 en Engels B2 op de in de bijlage 2 vastgestelde wijze.
C
Na bijlage 1 wordt een bijlage toegevoegd, als opgenomen in de bijlage bij deze regeling met het opschrift luidende als volgt:
Deze regeling zal met de toelichting in de Staatscourant worden geplaatst.
Het College voor Toetsen en Examens, de voorzitter, P.J.J. Hendrikse
Zoals gebruikelijk bij centrale examens, worden bij de centrale examens Engels B1 en B2 in het mbo cijfers toegekend. De manier waarop deze cijfers bepaald worden, noemen we ‘normering met een vaardigheidsschaal’.
Het gebruik van een vaardigheidsschaal is vooral geschikt als er meerdere varianten van een examen zijn. De ene variant kan net iets makkelijkere opgaven hebben dan de andere variant. Dit kan gebeuren omdat de moeilijkheid van een opgave niet heel precies ingeschat kan worden voordat deze is voorgelegd aan examenkandidaten. Bij het toekennen van cijfers moet daar rekening mee gehouden worden. Op de makkelijkere varianten moet een kandidaat dan iets meer vragen goed beantwoord hebben om een 6 te krijgen. We kunnen ook zeggen: een kandidaat moet eenzelfde vaardigheid aantonen voor een 6, ongeacht de variant die hij maakt, ongeacht het jaar waarin het examen wordt afgelegd dan wel de examenperiode binnen dat jaar. En dit moet ook gelden voor ieder ander cijfer. Ongeacht de variant die gemaakt wordt, moet eenzelfde aangetoonde vaardigheid steeds beloond worden met eenzelfde cijfer.
Het cijfer dat toegekend wordt, wordt dus bepaald door de vaardigheid die een kandidaat heeft. Deze vaardigheid kan hij aantonen door opgaven van een examen goed te maken. Het examen is daarmee een meetinstrument geworden van de vaardigheid van de kandidaat. En net zoals een thermometer een meetinstrument is van de temperatuur, op de Celsius- of Fahrenheit-schaal, zo spreken we ook van een vaardigheidsschaal.
De lengte van mensen meten we normaal gesproken met een meetlat. Stel dat die niet uitgevonden was, dan zouden we de hoogte van muurtjes kunnen gebruiken om de lengte van mensen te meten: wie erover heen kijkt, is langer dan degene die dat niet kan. Op analoge wijze kunnen we opgaven gebruiken om de vaardigheid van kandidaten te meten: wie de opgave goed maakt, is vaardiger dan degene die dat niet kan. In Figuur 1 is een vaardigheidsschaal afgebeeld. De vaardigheden van de kandidaten en de moeilijkheden van de opgaven zijn streepjes op eenzelfde meetlat ofwel schaal. Kandidaten met een hoge vaardigheid hebben een grotere kans om opgaven goed te maken dan kandidaten met een lagere vaardigheid. Omgekeerd, opgaven met een hoge moeilijkheid worden minder vaak goed gemaakt dan opgaven met een lage moeilijkheid.
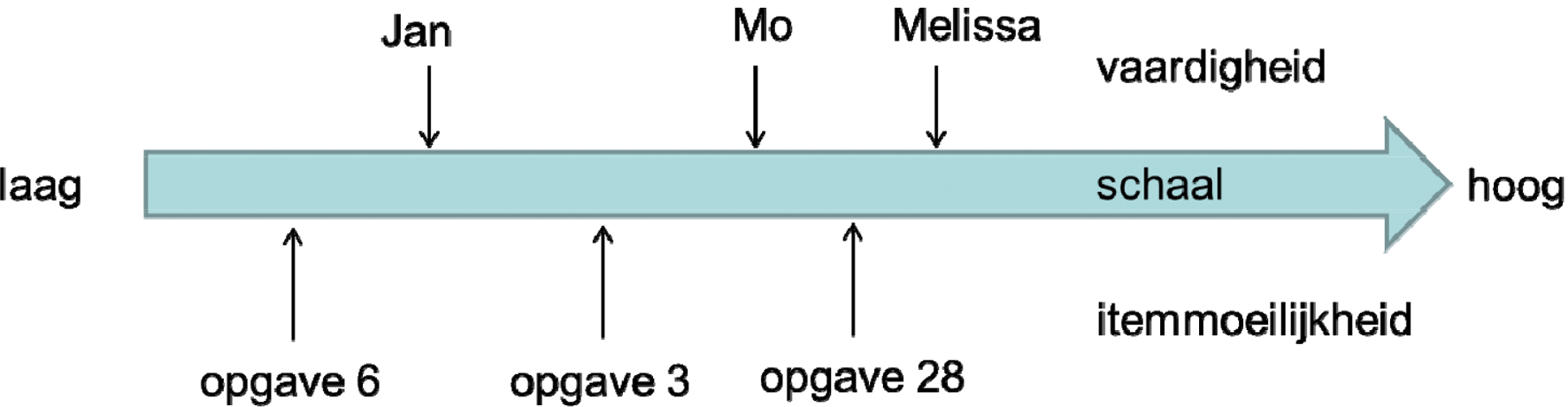
Figuur 1. Afbeelding van personen en opgaven op één vaardigheidsschaal
Een opgave heeft altijd dezelfde moeilijkheid; een examenvariant kan bestaan uit makkelijkere of moeilijkere opgaven. Een mini-examenvariant met alleen opgave 6 en opgave 3 uit bovenstaand voorbeeld, is bijvoorbeeld gemakkelijker dan een mini-examenvariant met alleen opgave 3 en opgave 28. Uit het antwoordgedrag van voldoende leerlingen op de makkelijke variant, kunnen we afleiden hoeveel makkelijker opgave 6 is dan opgave 3. Uit het antwoordgedrag van andere leerlingen op de moeilijke variant, kunnen we afleiden hoeveel moeilijker opgave 28 is dan opgave 3. Door een koppeling van deze twee verschillen, kunnen we afleiden hoeveel moeilijker opgave 28 is dan opgave 6. Op deze manier kunnen de moeilijkheden van alle opgaven op dezelfde schaal worden afgebeeld. Meer details over de schatting van itemmoeilijkheden staan in de sectie Schattingsmethode.
De schattingen van punten op de vaardigheidsschaal liggen vast op een lineaire transformatie na. We mogen bij alle punten dus een willekeurig aantal optellen, of alle punten met een willekeurige constante vermenigvuldigen. Een vaardigheidsschaal wordt geschat om scores op verschillende examenvarianten met elkaar te vergelijken. De precieze getallen die eraan hangen, zijn in wezen keuzes. Het nulpunt komt vrij willekeurig ergens te liggen. Negatieve vaardigheidsscores zijn lager dan vaardigheidsscore 0. Dit heeft geen inhoudelijke betekenis. We hadden bij alle scores ook 100 punten op kunnen tellen. In technische termen: de vaardigheidsschaal is van interval-niveau. Vergelijk met een temperatuur-schaal: het nulpunt op de Fahrenheit-schaal ligt ergens anders dan op de Celsius-schaal, maar voor beide geldt: hoe hoger, hoe warmer.
Je kunt bij temperatuur niet spreken van ‘het is vandaag twee keer zo warm als gisteren’, want voor zo’n uitspraak is een absoluut nulpunt nodig. Dat is er op de Fahrenheit- en Celsiusschaal niet. Zo kun je dus ook niet zeggen dat een kandidaat twee keer zo vaardig is als een andere kandidaat. Er is wel een inhoudelijke betekenis van negatieve graden op de Celsius-schaal (het vriest), maar op de Fahrenheit-schaal vriest het al onder 32 graden en is deze inhoudelijke betekenis van negatieve temperaturen er dus niet. Zo’n inhoudelijke betekenis van het nulpunt is er bij de vaardigheidsschaal ook niet.
Om nog technischer te worden: de ratio van twee verschillen is bij een interval-schaal wel interpreteerbaar. Dus als Jan, Mo, Mieke en Melissa respectievelijk 80, 90, 100 en 120 als vaardigheidsscores hebben, dan kun je wel zeggen dat het verschil in vaardigheid tussen de meisjes Mieke en Melissa (20 punten) twee keer zo groot is als het verschil tussen de jongens Jan en Mo (10 punten).
Als de moeilijkheden van alle opgaven of items in een examenperiode geschat zijn, wordt een beste schatting van de vaardigheid van een kandidaat gemaakt1 aan de hand van de items die de kandidaat daadwerkelijk zijn voorgelegd. Van alle antwoorden die een kandidaat geeft, wordt eerst de ruwe score berekend, ofwel het aantal behaalde punten. In combinatie met de itemkenmerken waarop deze ruwe score behaald is, wordt de vaardigheid geschat. Dit gebeurt per examenvariant voor iedere ruwe score apart, zie bijvoorbeeld tabel 1 voor een gedeelte van de omzettingstabel van score naar vaardigheid bij variant 2 van een toets of examen. De relatie tussen score en vaardigheid hoeft niet rechtlijnig te zijn. Dit hangt af van de onderlinge verschillen in moeilijkheid tussen de opgaven.
|
Variant |
Score |
Vaardigheid |
|---|---|---|
|
... |
... |
|
|
V2 |
14 |
335 |
|
V2 |
15 |
349 |
|
V2 |
16 |
363 |
|
V2 |
17 |
376 |
|
V2 |
18 |
389 |
|
V2 |
19 |
402 |
|
V2 |
20 |
415 |
|
… |
… |
Deze methode levert dus per examenvariant een tabel op met achter iedere mogelijke ruwe score een vaardigheidsschatting. De ruwe score loopt van 0 tot en met de maximale score. De vaardigheidsschatting heeft niet overal dezelfde nauwkeurigheid. Bij de allerlaagste en allerhoogste scores is de meetnauwkeurigheid lager dan ergens in het midden van de scores. De exacte score waarbij de meetnauwkeurigheid het hoogst is, hangt af van de moeilijkheid van de opgaven in de examenvariant.
Als er opgaven in een examenvariant zitten, waarover de normeringsvergadering beslist dat zij niet mee mogen tellen bij de beoordeling van een kandidaat, dan noemen we dit geneutraliseerde items. Alle kandidaten krijgen voor een geneutraliseerd item het maximale aantal punten dat behaald kan worden. Bij de schatting van de itemparameters doen de geneutraliseerde items niet mee, alleen de antwoorden op de overige items worden gebruikt voor het vaststellen van de vaardigheidsschaal. Bij de schatting worden de geneutraliseerde items buiten beschouwing gelaten.
De vaardigheid van de kandidaat wordt dus eigenlijk geschat aan de hand van de antwoorden op een verkorte examenvariant, waarin de geneutraliseerde items niet opgenomen zijn. In tabel 2 staat een voorbeeld van de omzettingstabel van score naar vaardigheid als er in een variant, waarop maximaal 40 punten behaald kunnen worden, drie geneutraliseerde items van ieder maximaal 1 punt zijn. De schatting van de vaardigheid gaat uitsluitend over de verkorte variant, met scores 0 tot en met 37. De rapportage gaat over de gehele range 0 tot en met 40. De ‘neutrale punten’ worden bij de verkorte score opgeteld om tot de score op de volledige variant te komen. In de rapportage-tabel staat achter de scores 0, 1 en 2 dezelfde vaardigheid als bij de laagst mogelijke score 3, namelijk vaardigheid 0. Echter, in praktijk komen deze scores niet voor omdat iedere kandidaat minimaal 3 punten scoort, namelijk op de geneutraliseerde items.
|
Schatting |
Rapportage |
||
|---|---|---|---|
|
Score verkorte variant |
Vaardigheid |
Score volledige variant |
Vaardigheid |
|
Nvt |
nvt |
0 |
0 |
|
Nvt |
nvt |
1 |
0 |
|
Nvt |
nvt |
2 |
0 |
|
0 |
0 |
3 |
0 |
|
1 |
0 |
4 |
0 |
|
2 |
18 |
5 |
18 |
|
.. |
.. |
.. |
|
|
37 |
999 |
40 |
999 |
Noot. Gerapporteerde scores 0,1 en 2 komen niet voor, vanwege de geneutraliseerde items.
Door middel van item respons theorie-schaling worden alle kandidaten en opgaven op dezelfde vaardigheidsschaal afgebeeld. Cijfers reflecteren de waardering voor behaalde vaardigheid. Het belangrijkste punt op de vaardigheidsschaal is de cesuur: vanaf de cesuur-vaardigheid wordt de vaardigheid van kandidaten als voldoende beoordeeld. Een vaardigheid onder de cesuur wordt als onvoldoende beoordeeld.
Om afrondingsproblemen te voorkomen, is het precieze cijfer dat wordt toegekend bij de cesuur-vaardigheid afhankelijk van het aantal gerapporteerde decimalen. Als hele cijfers gerapporteerd worden, zoals bij de Rekentoets vo of het centraal examen Rekenen, is het cijfer bij de cesuur een 5,5. Als cijfers met één decimaal worden gerapporteerd, zoals bij de centrale examens Nederlands en Engels, is het cijfer bij de cesuur gelijk aan 5,45. In Figuur 2 is dit bij vaardigheid 492 voor een voldoende cijfer op B2-niveau.
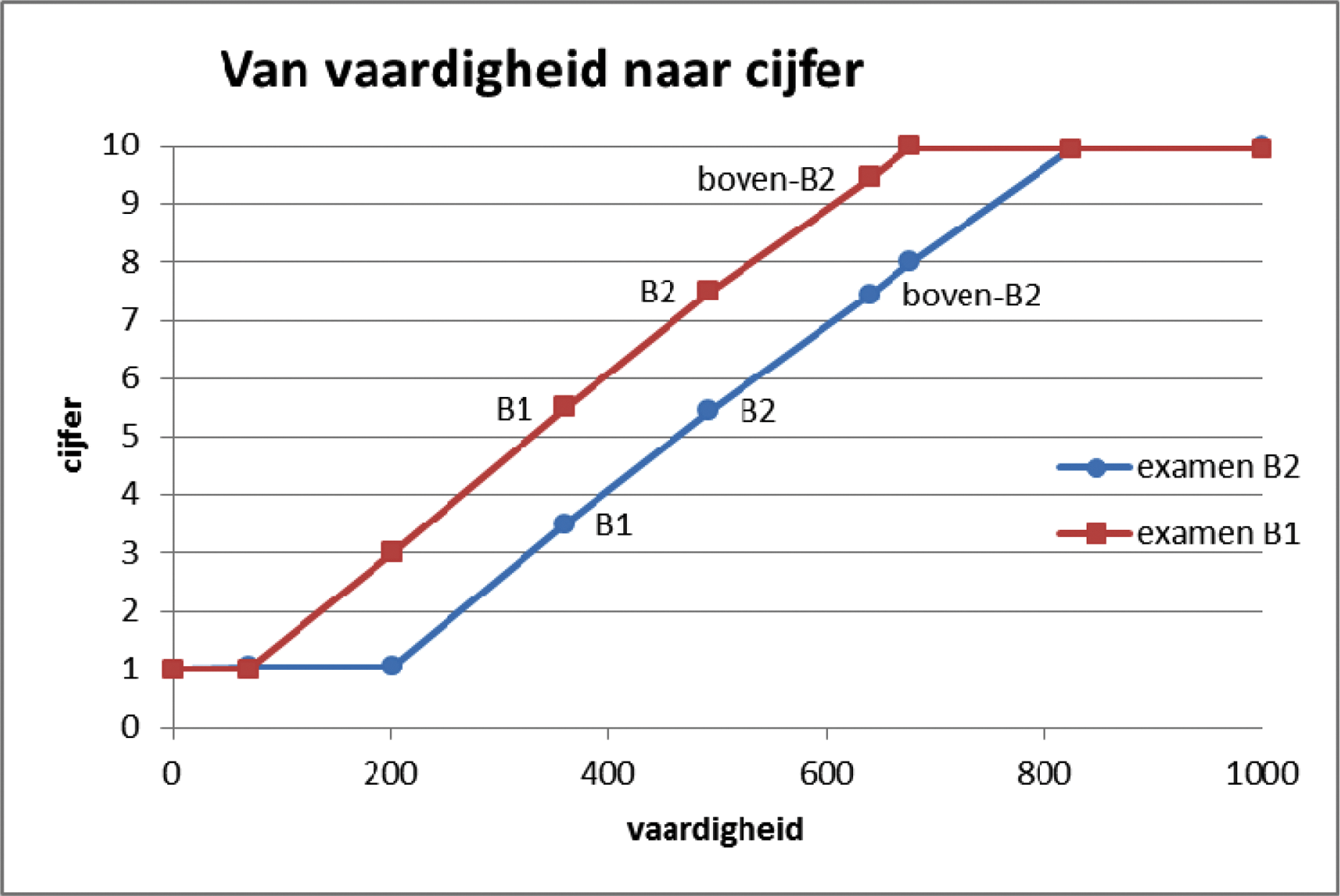
Figuur 2. Voorbeeld van omzetting van vaardigheidsscores naar cijfers
De omzetting van vaardigheid naar cijfer is lineair met een knik. Dat wil zeggen dat er een rechtlijnig verband is tussen cijfer en vaardigheid boven het ERK-niveau B2 en dat er een ander rechtlijnig verband is onder het ERK-niveau B2. Bij de normering worden in totaal drie punten op de vaardigheidsschaal vastgelegd. Bij de centrale examens Engels B1 en B2 zijn dit de ERK-niveaus B1, B2 en boven-B2. In het examen B1-Engels corresponderen deze punten respectievelijk met de cijfers 5,5, 7,5 en 9,5 en in het examen B2-Engels met de cijfers 3,5, 5,5 en 7,5.
De drie punten op de vaardigheidsschaal die de omzetting van vaardigheid naar cijfer bepalen, noemen we ook wel standaarden. De rechte lijnen die door de drie punten bepaald worden, worden naar boven en beneden afgekapt. Cijfer boven 10,0 en onder 1,0 worden immers niet toegekend. Voor de centrale examens mbo Engels zijn deze standaarden bepaald door de ERK-niveaus, zoals vastgesteld op de centrale examens VO Engels 2012, via een posttest over te brengen.
Om de moeilijkheid van de opgaven precies te schatten, wordt gebruik gemaakt van item respons theorie (IRT). Opgaven worden binnen deze theorie items genoemd. De antwoorden van leerlingen worden responsen genoemd. De kans dat een bepaalde kandidaat een bepaald item goed beantwoordt, is afhankelijk van de vaardigheid van de persoon en van kenmerken van het item, zoals de moeilijkheid ervan. De vaardigheid van een kandidaat wordt met de Griekse letter θ aangeduid. De kans dat een kandidaat met een vaardigheid θ een item goed maakt, wordt omschreven met een wiskundige formule of functie. Van de familie van modellen die binnen de IRT vallen, wordt in dit geval het one parameter logistic model (OPLM, Glas & Verhelst, 1989, Verhelst & Glas, 1993; Verhelst, Glas & Verstralen, 1993; Eggen & Verhelst, 2011) gebruikt. De itemresponsfunctie van het OPLM is gegeven door
waarin αi de zogenaamde discriminatie-index van het item is, en βi de moeilijkheidsparameter van item i is. In Figuur 3 zijn de itemresponscurven weergegeven van twee items i en j, die even moeilijk zijn maar verschillend discrimineren. Als de vaardigheid van de kandidaat gelijk is aan de moeilijkheid van een opgave, dan heeft hij een kans van 50% om de opgave goed te maken. Opgaven met een hoge discriminatie-index onderscheiden beter tussen hoog- en laagvaardige kandidaten, ofwel de kans om een opgave goed te maken, neemt hierbij snel toe met θ. De index αi wordt ook wel de hellingsparameter genoemd.
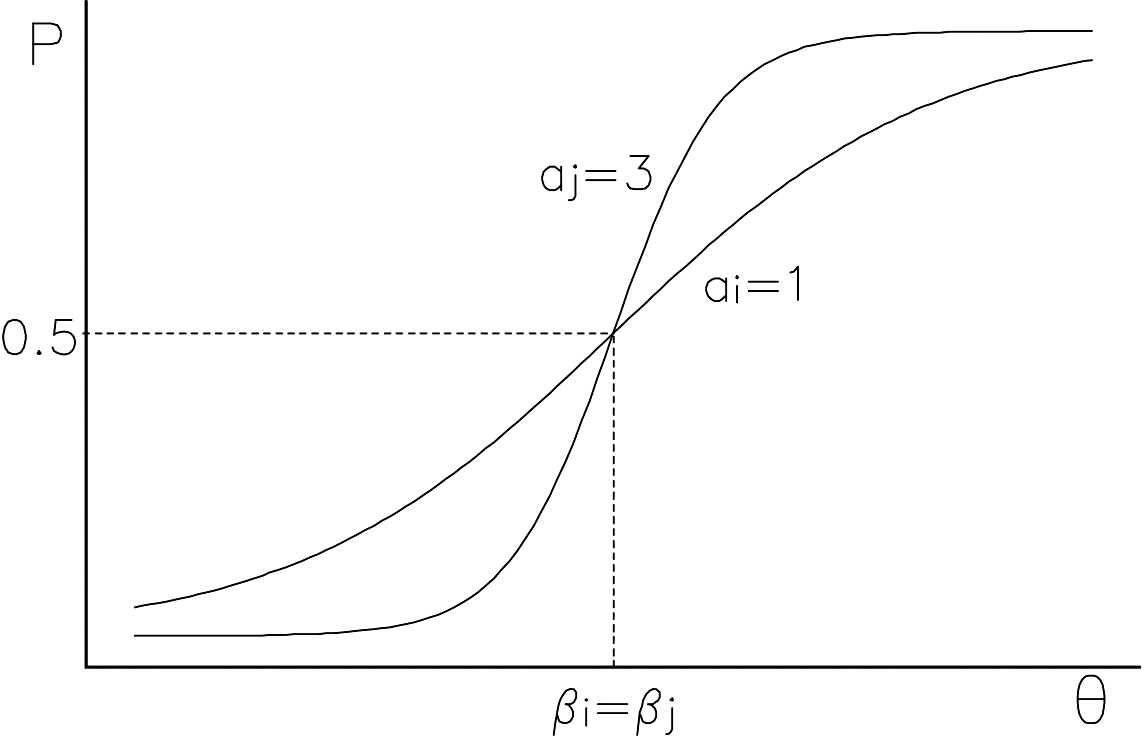
Figuur 3. Twee itemresponscurven in het OPLM: zelfde moeilijkheid, verschillende discriminatie-index
Een vaak toegepaste schattingsmethode voor de moeilijkheidsparameters βi is de ‘conditionele grootste aannemelijkheidsmethode’ (in het Engels: Conditional Maximum Likelihood, verder aangeduid als CML). Die maakt gebruik van het feit dat in het model een afdoende steekproefgrootheid ('sufficient statistic') bestaat voor de latente variabele θ, namelijk de ruwe score of het aantal correct beantwoorde items. Dat betekent grofweg dat, indien de itemparameters bekend zijn, alle informatie die het antwoordpatroon over de vaardigheid bevat, kan worden samengevat in de ruwe score; het doet er dan verder niet meer toe welke opgaven goed en welke fout zijn gemaakt. Hieruit vloeit voort dat de conditionele kans op een juist antwoord op item i, gegeven de ruwe score, een functie is die alleen afhankelijk is van de itemparameters en onafhankelijk van de waarde van θ2. De CML-schattingsmethode maakt van deze functie gebruik. Deze methode maakt geen enkele vooronderstelling over de verdeling van de vaardigheid in de populatie, en is ook onafhankelijk van de wijze waarop de steekproef is getrokken. Door de indices αi te beperken tot (positieve) gehele getallen, en door ze a priori als constanten in te voeren, is het mogelijk CML-schattingen van de itemparameters βi te maken.
Eggen, T. J. H. M., & Verhelst, N. D. (2011). Item calibration in incomplete testing designs. Psicologica: International Journal of Methodology and Experimental Psychology, 32, 107–132.
Glas, C. A. W., & Verhelst, N.D. (1989). Extensions of the partial credit model, Psychometrika, 54, 635–659.
Verhelst, N.D., & Engelen, R.J.H. (1999). An ability estimator in the two parameter logistic model based on raw scores. Research memorandum. Arnhem: Cito.
Verhelst, N.D., & Glas, C.A.W. (1993). A dynamic generalization of the Rasch model. Psychometrika, 58, 395–415.
Verhelst, N.D., Glas, C.A.W., & Verstralen, H.H.F.M. (1993). OPLM: One parameter logistic model. Computer program and manual. Arnhem: Cito.
Warm, T.A. (1989). Weighted likelihood estimation of ability in item response theory. Psychometrika, 54, 427–450.
De ‘Regeling omzetting scores in cijfers bij centrale examinering mbo (2015)’ wordt middels deze wijziging aangevuld met een nieuwe bijlage betreffende de omzetting van score naar cijfer van de centrale examens Engels B1 en Engels B2 in het mbo. Vanaf 1 augustus 2017 is deelname aan het centraal examen Engels B1 verplicht voor mbo-4-studenten en krijgen zij daarnaast de mogelijkheid om het centraal examen Engels ook op het niveau B2 af te leggen. De oude regeling voorzag alleen in een beschrijving voor de omzetting score naar cijfer voor het centraal examen Nederlandse taal en rekenen. De nieuwe regeling omschrijft tevens de wijze waarop een schaalscore op het ERK-referentieniveau B1 en B2 leidt tot een corresponderend cijfer op de tienpuntsschaal. De regeling is bedoeld voor de examencommissie ten behoeve van het bepalen van het resultaat op het centraal examen Engels B1 en B2 voor mbo-4-studenten.
Realiseert de vernummering van het bestaande artikel 1 in artikel 1, eerste lid. Hierbij wordt ingevoegd dat het specifiek de in de bijbehorende bijlage aangegeven centrale examens Nederlandse taal en rekenen in het mbo betreft. Onderdeel 4 voorziet de opname van een nieuw tweede lid bij artikel 1 in de Regeling omzetting scores in cijfers bij centrale examinering mbo (2015), betreffende de omzetting van score naar cijfer van de centrale examens Engels B1 en Engels B2 in het mbo.
Regelt de vernummering van de bestaande bijlage in bijlage 1 behorend bij artikel 1, eerste lid.
Voorziet in de toevoeging van bijlage 2 aan de Regeling omzetting scores in cijfers bij centrale examinering mbo (2015), behorende bij artikel 1, tweede lid. Het betreft de wijze van omzetting van score naar cijfer voor de centrale examens Engels B1 en Engels B2 in het mbo.
Het College voor Toetsen en Examens, de voorzitter, P.J.J. Hendrikse
De gebruikte schatting is een weighted maximum likelihood (WML) schatter bij de ongewogen score. Verhelst en Engelen (1999) tonen aan dat dit een veralgemenisering is van de WML-schatter bij gewogen scores (Warm, 1989).
Kopieer de link naar uw clipboard
https://zoek.officielebekendmakingen.nl/stcrt-2017-31868.html
De hier aangeboden pdf-bestanden van het Staatsblad, Staatscourant, Tractatenblad, provinciaal blad, gemeenteblad, waterschapsblad en blad gemeenschappelijke regeling vormen de formele bekendmakingen in de zin van de Bekendmakingswet en de Rijkswet goedkeuring en bekendmaking verdragen voor zover ze na 1 juli 2009 zijn uitgegeven. Voor pdf-publicaties van vóór deze datum geldt dat alleen de in papieren vorm uitgegeven bladen formele status hebben; de hier aangeboden elektronische versies daarvan worden bij wijze van service aangeboden.
